京都大学 理学部特色入試 2022年度 第2問 解説
(2021年11月に行われた特色入試の問題です。2022年に行われた特色入試の問題はこちら)
問題編
問題
半径 $1$ の円 $C$ の周上に相異なる5点 $A_1,A_2,A_3,A_4,A_5$ がこの順に並んでいるとし、
$B_1$ を線分 $A_1A_3$ と線分 $A_2A_4$ の交点、
$B_2$ を線分 $A_2A_4$ と線分 $A_3A_5$ の交点、
$B_3$ を線分 $A_3A_5$ と線分 $A_4A_1$ の交点、
$B_4$ を線分 $A_4A_1$ と線分 $A_5A_2$ の交点、
$B_5$ を線分 $A_5A_2$ と線分 $A_1A_3$ の交点
とするとき、
$S_1$ を $\triangle A_1B_5B_4$ の面積、
$S_2$ を $\triangle A_2B_1B_5$ の面積、
$S_3$ を $\triangle A_3B_2B_1$ の面積、
$S_4$ を $\triangle A_4B_3B_2$ の面積、
$S_5$ を $\triangle A_5B_4B_3$ の面積、
$T$ を五角形 $B_1B_2B_3B_4B_5$ の面積
とおく。このように $A_1,A_2,A_3,A_4,A_5$ を動かしたとき、\[ S=S_1+S_2+S_3+S_4+S_5+2T \]の最大値を求めよ。
ただし、三角比の値は具体的に求めずに用いてよい。
考え方
問題文が長いですが、図をかいてみると、状況はシンプルだとわかります。何を考えないといけないかはすぐにわかります。また、最大となるのはどのようなときであるかも、すぐに予想できます。
問題はどうやって示すかです。5点が同時に動くのを考えるのは大変なので、図形的な性質から候補をしぼっていくことを考えましょう。点の配置の候補をしぼってから、変数を使って面積を表すことを考えましょう。
解答編
問題
半径 $1$ の円 $C$ の周上に相異なる5点 $A_1,A_2,A_3,A_4,A_5$ がこの順に並んでいるとし、
$B_1$ を線分 $A_1A_3$ と線分 $A_2A_4$ の交点、
$B_2$ を線分 $A_2A_4$ と線分 $A_3A_5$ の交点、
$B_3$ を線分 $A_3A_5$ と線分 $A_4A_1$ の交点、
$B_4$ を線分 $A_4A_1$ と線分 $A_5A_2$ の交点、
$B_5$ を線分 $A_5A_2$ と線分 $A_1A_3$ の交点
とするとき、
$S_1$ を $\triangle A_1B_5B_4$ の面積、
$S_2$ を $\triangle A_2B_1B_5$ の面積、
$S_3$ を $\triangle A_3B_2B_1$ の面積、
$S_4$ を $\triangle A_4B_3B_2$ の面積、
$S_5$ を $\triangle A_5B_4B_3$ の面積、
$T$ を五角形 $B_1B_2B_3B_4B_5$ の面積
とおく。このように $A_1,A_2,A_3,A_4,A_5$ を動かしたとき、\[ S=S_1+S_2+S_3+S_4+S_5+2T \]の最大値を求めよ。
ただし、三角比の値は具体的に求めずに用いてよい。
解答
図は次のようになっている。
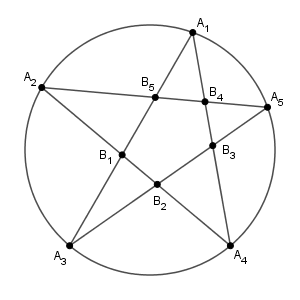
円 $C$ の中心を $O$ とする。以下では、まず、$S$ の最大値を求めるには、点 $O$ が五角形 $B_1B_2B_3B_4B_5$ 内にある場合だけを考えればよいことを示す。
\begin{eqnarray} & & \angle A_1 +\angle A_2 +\angle A_3 +\angle A_4 +\angle A_5 \\[5pt] &=& \angle A_3B_2A_4 +\angle A_4A_2A_5 +\angle A_2A_5A_3 \\[5pt] &=& 180^{\circ} \end{eqnarray}が成り立つ。よって、 $\angle A_1OA_2$, $\angle A_2OA_3$, $\angle A_3OA_4$, $\angle A_4OA_5$, $\angle A_5OA_1$ のうち、少なくとも1つは $180^{\circ}$ 未満である。 $\angle A_3OA_4$ が $180^{\circ}$ 未満としても一般性を失わないので、以下ではこれを仮定する。$A_3A_3'$, $A_4A_4'$ が直径となるように点 $A_3'$, $A_4'$ をとる。
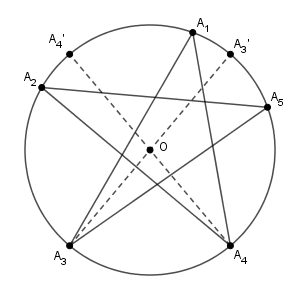
もし、 $A_2$ が弧 $A_3'A_4'$ 上にあるとする。

このとき、 $|\triangle XYZ|$ で三角形 $XYZ$ の面積を表すことにすると、
\begin{eqnarray}
S
&=&
|\triangle A_1A_3B_3| +|\triangle A_2A_4A_5| -|\triangle B_3A_4A_5|
\end{eqnarray}と表すことができる。ここで、点 $A_2$ を動かしても、線分 $A_1A_3,A_1A_4,A_3A_5$ は動かないため、 $|\triangle A_1A_3B_3|$, $|\triangle B_3A_4A_5|$ は変化しない。また、点 $A_2$ を $A_4'$ に移動すると、 $\angle A_4A_2A_5$ は不変で、線分 $A_2A_4$ と $A_2A_5$ は大きくなるため、 $|\triangle A_2A_4A_5|$ は大きくなる。よって、 $S$ の最大値を求めるには、点 $A_2$ は弧 $A_3A_4'$ 上にある場合を考えるだけでよい。同様に、点 $A_5$ は弧 $A_4A_3'$ 上にある場合を考えるだけでよい。以下では、点 $A_2,A_5$ はこの場合だけを考える。

($A_2$ は弧 $A_3A_4'$ 上にあり、 $A_5$ は弧 $A_4A_3'$ 上にある場合を考える)
次に、$A_1$ だけを動かすことを考える。
\begin{eqnarray}
S
&=&
|\triangle A_2A_5B_2| +|\triangle A_1A_3A_4| -|\triangle B_2A_3A_4|
\end{eqnarray}と表すことができる。ここで、線分 $A_2A_4,A_3A_5,A_5A_2$ は動かないため、 $|\triangle A_2A_5B_2|$, $|\triangle B_2A_3A_4|$ は変化しない。よって、 $S$ が最大になるのは $|\triangle A_1A_3A_4|$ が最大になるときであり、 $A_1A_3=A_1A_4$ のときであることがわかる。 $A_1$ は線分 $A_3A_4$ の垂直二等分線上にとればよく、 $A_2,A_5$ の位置関係から必ず $A_1$ を動かすことができる。
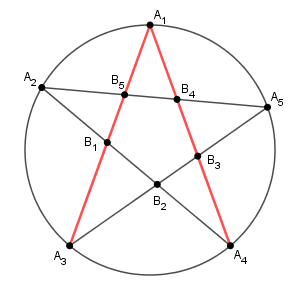
( $A_1$ だけを動かす場合は、赤い2つの辺の長さが等しくなるときに $S$ が最大となる)
以下では、 $A_1$ は $A_1A_3=A_1A_4$ を満たすように動かしたと仮定する。
次に、 $A_2$ だけを動かすことを考える。 $A_1$ のときと同様に考えると、 $A_2$ が線分 $A_4A_5$ の垂直二等分線上にあるときに $S$ は最大となる。 $A_5$ は弧 $A_4A_3'$ 上にあるので、線分 $A_4A_5$ の垂直二等分線と円周との交点は、弧 $A_3A_4'$ 上にあるため、必ず $A_2$ を動かすことができる。
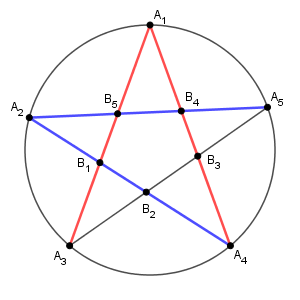
(赤い辺の長さが等しく、青い辺の長さが等しくなるときに $S$ が最大となる)
以上より、 $S$ の最大値を求めるには、 $A_1A_3=A_1A_4$ かつ $A_2A_4=A_2A_5$ の場合のみを考えればよい。以下では、この場合について考える。
点 $A_1$ は線分 $A_3A_4$ の垂直二等分線上にあるため、点 $O$ は、「線分 $A_1A_3$ 、線分 $A_1A_4$ 、弧 $A_3A_4$ で囲まれた部分」の中にある。また、点 $A_2$ は線分 $A_4A_5$ の垂直二等分線上にあるため、点 $O$ は、「線分 $A_2A_4$ 、線分 $A_2A_5$ 、弧 $A_4A_5$ で囲まれた部分」の中にある。また、 $A_5$ は弧 $A_4A_3'$ 上にあるようにとっている。以上のことから、点 $O$ は五角形 $B_1B_2B_3B_4B_5$ 内(辺上の点を含む)にあることがわかる。

ここで、 $\angle OA_1A_3=\frac{\alpha_1}{2}$, $\angle OA_2A_4=\frac{\alpha_2}{2}$, $\angle OA_3A_5=\frac{\alpha_3}{2}$, $\angle OA_4A_1=\frac{\alpha_4}{2}$, $\angle OA_5A_2=\frac{\alpha_5}{2}$ とおくと、\[ \alpha_1+\alpha_2+\alpha_3+\alpha_4+\alpha_5=180^{\circ} \]が成り立つ。また、
\begin{eqnarray}
& &
|\triangle OA_1A_3|+|\triangle OA_2A_4|+|\triangle OA_3A_5| \\
& & +|\triangle OA_4A_1|+|\triangle OA_5A_2| \\[5pt]
&=&
|\triangle OA_1B_5|+|\triangle OB_5B_1|+|\triangle OB_1A_3| \\
& & +|\triangle OA_2B_1|+|\triangle OB_1B_2|+|\triangle OB_2A_4| \\
& & +|\triangle OA_3B_2|+|\triangle OB_2B_3|+|\triangle OB_3A_5| \\
& & +|\triangle OA_4B_3|+|\triangle OB_3B_4|+|\triangle OB_4A_1| \\
& & +|\triangle OA_5B_4|+|\triangle OB_4B_5|+|\triangle OB_5A_2| \\
&=&
|\triangle OA_1B_5|+|\triangle OB_1A_3| \\
& & +|\triangle OA_2B_1|+|\triangle OB_2A_4| \\
& & +|\triangle OA_3B_2|+|\triangle OB_3A_5| \\
& & +|\triangle OA_4B_3|+|\triangle OB_4A_1| \\
& & +|\triangle OA_5B_4|+|\triangle OB_5A_2| \\
& & +T \\
&=&
S_1+S_2+S_3+S_4+S_5+T +T=S \\
\end{eqnarray}となる。ここで、\[ |\triangle OA_1A_3|=\frac{\sin\frac{\alpha_1}{2}\cdot 2\cos\frac{\alpha_1}{2} }{2}=\frac{\sin\alpha_1}{2} \]と計算できるので、他も同様にすると
\begin{eqnarray}
S
&=&
|\triangle OA_1A_3|+|\triangle OA_2A_4|+|\triangle OA_3A_5| \\
& & +|\triangle OA_4A_1|+|\triangle OA_5A_2| \\[5pt]
&=&
\frac{\sin\alpha_1}{2}+\frac{\sin\alpha_2}{2}+\frac{\sin\alpha_3}{2}+\frac{\sin\alpha_4}{2}+\frac{\sin\alpha_5}{2}
\end{eqnarray}が成り立つ。 $f(x)=\sin x$ は上に凸だから、イェンセンの不等式(下の解説参照)より
\begin{eqnarray}
& &
\frac{\sin\alpha_1}{5}+\frac{\sin\alpha_2}{5}+\frac{\sin\alpha_3}{5}+\frac{\sin\alpha_4}{5}+\frac{\sin\alpha_5}{5} \\[5pt]
&\leqq &
\sin\frac{\alpha_1+\alpha_2+\alpha_3+\alpha_4+\alpha_5}{5} = \sin 36^{\circ}
\end{eqnarray}である(等号はすべての角が $36^{\circ}$ のときに成り立つ)ので、$S$ が最大となるのは、五角形 $A_1A_2A_3A_4A_5$ が正五角形のときであり、その値は $\dfrac{5}{2}\sin 36^{\circ}$ と求められる。
(終)
解説
5つの点が動くので、 $A_1(1,0)$, $A_2(\cos\theta_2, \sin\theta_2)$ などとしたくなりますが、変数が多すぎます。また、角を決めたところで、面積を表すのも難しいです。そのため、図形的な性質を用いて、シンプルな状況にしぼってから考えたほうがいいでしょう。
式などを使わなくても、円に内接する三角形で、1点だけを動かしたときにいつ最大になるかを求めることはできます。これを利用して点の配置の候補をしぼります。
終盤でイェンセンの不等式を使っています。この内容は以下の通りです。 $f(x)$ が上に凸である関数とし、 $p_1,p_2,\cdots,p_n$ を和が $1$ となる正の実数とします。また、 $x_1,x_2,\cdots,x_n$ を実数の列とします。このとき、次の不等式が成り立ちます。\[ \sum_{i=1}^n p_i f(x_i) \leqq f\left(\sum_{i=1}^n p_ix_i\right) \]上の解答では、 $p_i$ たちを $\dfrac{1}{5}$ として適用しています。
以下では、イェンセンを使わない方法も示しておきます。(実質的に、イェンセンの不等式の特殊ケースを証明していることになります)
$y=\sin x$ の $x=36^{\circ}$ における接線を $y=ax+b$ とします。このとき、 $a\cdot \frac{\pi}{5}+b=\sin 36^{\circ}$ が成り立ちます。 $f(x)=ax+b-\sin x$ とすると、 $f'(x)=a-\cos x$ で、 $f^{\prime\prime}(x)=\sin x$ なので、 $0^{\circ}\lt x\lt 180^{\circ}$ の範囲では、 $f'(x)$ は単調増加です。また、 $f'(36^{\circ})=0$ であり、 $f(36^{\circ})=0$ なので、\[ ax+b \geqq \sin x \]が成り立ちます。等号は、 $x=36^{\circ}$ のときに成り立ちます。ここで、 $x=\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5$ として辺々足すと\[ a\sum_{i=1}^5 \alpha_i +b \geqq \sum_{i=1}^5 \sin \alpha_i \]が得られます。両辺を $5$ で割り、 $\displaystyle \sum _{i=1}^5 \alpha_i=180^{\circ}$ であることも使うと\[ a\cdot \frac{\pi}{5}+b \geqq \sum_{i=1}^5 \frac{\sin \alpha_i}{5} \]が得られます。ここで、左辺は $\sin 36^{\circ}$ であり、等号はすべての角が $36^{\circ}$ のときに成り立つことから、上の解答のように最大値が求められます。





