京都大学 理学部特色入試 2023年度 第1問 解説
(2022年11月に行われた特色入試の問題です。2023年に行われた特色入試の問題はこちら)
問題編
問題
平面内の鋭角三角形 $\triangle \mathrm{ABC}$ を考える。 $\triangle \mathrm{ABC}$ の内部の点 $\mathrm{P}$ に対して、
直線 $\mathrm{BC}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{D}$、
直線 $\mathrm{CA}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{E}$、
直線 $\mathrm{AB}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{F}$とする。6点 $\mathrm{A,B,C,D,E,F}$ が同一円周上にあるような $\mathrm{P}$ は $\triangle \mathrm{ABC}$ の内部にいくつあるか求めよ。
考え方
点 $\mathrm{P}$ を決めて $\mathrm{D,E,F}$ がどうなるか、と考えるよりも、 $\mathrm{D,E,F}$ が条件を満たすような $\mathrm{P}$ はどんな点か、と考えたほうが解きやすいでしょう。そうすると、条件が強すぎて、条件を満たすような点の候補は、実はすごく少ないことがわかります。
あとは、逆に、条件を満たすような点 $\mathrm{P}$ が存在することを示します。
図形がごちゃごちゃしやすく、図のかきかたによっては変な思い込みをしてしまう可能性もあるので、適宜、図をかきなおしながら考えましょう。
解答編
問題
平面内の鋭角三角形 $\triangle \mathrm{ABC}$ を考える。 $\triangle \mathrm{ABC}$ の内部の点 $\mathrm{P}$ に対して、
直線 $\mathrm{BC}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{D}$、
直線 $\mathrm{CA}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{E}$、
直線 $\mathrm{AB}$ に関して $\mathrm{P}$ と対称な点を $\mathrm{F}$とする。6点 $\mathrm{A,B,C,D,E,F}$ が同一円周上にあるような $\mathrm{P}$ は $\triangle \mathrm{ABC}$ の内部にいくつあるか求めよ。
解答
$\triangle \mathrm{ABC}$ の外心を $\mathrm{O}$ とし、外接円 $\mathrm{O}$ の半径を $R$ とする。
また、この外接円を、直線 $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ について対称移動したとき、点 $\mathrm{O}$ が移動する点を、それぞれ、点 $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ とおく。
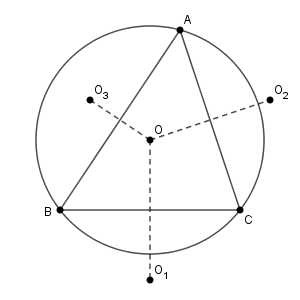
6点 $\mathrm{A,B,C,D,E,F}$ が同一円周上にあるとき、その円は円 $\mathrm{O}$ である。ここで、点 $\mathrm{D}$ が円 $\mathrm{O}$ の円周上にあることと、点 $\mathrm{P}$ が円 $\mathrm{O}_1$ 上にあることは同値である。
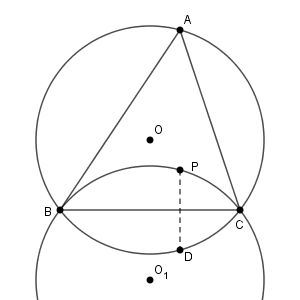
同様に考えると、 $\mathrm{D,E,F}$ が円 $\mathrm{O}$ の円周上にあることは、点 $\mathrm{P}$ が円 $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ の円周(下の図の赤い3つの円)上にあることと同値である。

以上から、点 $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ からの距離がいずれも $R$ となるような $\triangle \mathrm{ABC}$ の内部の点があれば、その点は点 $\mathrm{P}$ の条件を満たし、このとき以外に条件を満たすことはない。なお、このことから、点 $\mathrm{P}$ は少なくとも $\triangle \mathrm{O_1O_2O_3}$ の外心なので、条件を満たす点 $\mathrm{P}$ は存在するなら1点しかない。
以下では、このような点が必ず存在することを示す。
四角形 $\mathrm{BOCO_1}$ はすべての辺の長さが $R$ なので、ひし形である(なお、 $\triangle\mathrm{ABC}$ は鋭角三角形なので、外心が辺上にあることはない)。同様に、四角形 $\mathrm{COAO_2}$ と四角形 $\mathrm{AOBO_3}$ もひし形である。
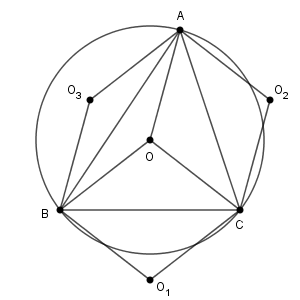
よって、$\overrightarrow{\mathrm{O_1O_2}} = \overrightarrow{\mathrm{O_1C}}+\overrightarrow{\mathrm{CO_2}} = \overrightarrow{\mathrm{BO}}+\overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{BA}}$ となる。同様に、 $\overrightarrow{\mathrm{O_2O_3}}=\overrightarrow{\mathrm{CB}}$, $\overrightarrow{\mathrm{O_3O_1}}=\overrightarrow{\mathrm{AC}}$ が成り立つ。
$\mathrm{O_1O_2}$ と $\mathrm{AB}$ は平行なので、線分 $\mathrm{O_1O_2}$ の垂直二等分線は直線$\mathrm{AB}$ とも垂直である。また、三角形 $\mathrm{CO_1O_2}$ は二等辺三角形なので、線分 $\mathrm{O_1O_2}$ の垂直二等分線は点 $\mathrm{C}$ を通る。よって、線分 $\mathrm{O_1O_2}$ の垂直二等分線は、点 $\mathrm{C}$ から直線 $\mathrm{AB}$ におろした垂線と一致する。
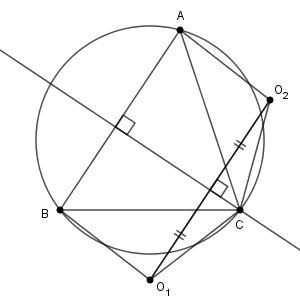
同様に、線分 $\mathrm{O_2O_3}$ の垂直二等分線は、点 $\mathrm{A}$ から直線 $\mathrm{BC}$ におろした垂線と一致する。また、線分 $\mathrm{O_3O_1}$ の垂直二等分線は、点 $\mathrm{B}$ から直線 $\mathrm{CA}$ におろした垂線と一致することがわかる。これより、 $\triangle \mathrm{O_1O_2O_3}$ の外心は、 $\triangle \mathrm{ABC}$ の垂心と一致することがわかる。
$\overrightarrow{\mathrm{O_1O_2}}=\overrightarrow{\mathrm{BA}}$ などから、3辺の長さがそれぞれ等しいことより、 $\triangle \mathrm{O_1O_2O_3}$ と $\triangle \mathrm{ABC}$ は合同であることがわかる。よって、 $\triangle \mathrm{O_1O_2O_3}$ の外接円の半径は、 $\triangle \mathrm{ABC}$ の外接円の半径と等しく、 $R$ である。なので、$\triangle \mathrm{ABC}$ の垂心は、点 $\mathrm{O}_1, \mathrm{O}_2, \mathrm{O}_3$ からの距離がいずれも $R$ である。
また、 $\triangle \mathrm{ABC}$ は鋭角三角形なので、垂心は三角形の内部にある。
以上より、 $\triangle \mathrm{ABC}$ の垂心は、必ず点 $\mathrm{P}$ の条件を満たし、これ以外に条件を満たす点はない。よって、条件を満たす点は、1個。
(終)





