京都大学 理学部特色入試 2023年度 第3問 解説
(2022年11月に行われた特色入試の問題です。2023年に行われた特色入試の問題はこちら)
問題編
問題
複素数の数列 $\{z_n\}$ に対する次の2つの条件を考える。
(i) すべての自然数 $n$ に対して、 $|z_n-z_{n+1}|=2^n$ が成り立つ。
(ii) すべての自然数 $n$ に対して、\[ \frac{(z_n-z_{n+1})(z_{n+2}-z_{n+3})}{ (z_{n+1}-z_{n+2})(z_{n+3}-z_{n}) } \] は実数である。
複素数の数列 $\{z_n\}$ で (i) と (ii) をともに満たすものをすべて考えたとき、\[ \frac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}} \]がとり得る値をすべて求めよ。
考え方
(ii)の条件が強そうなので、これを利用しましょう。図形的に考えて、 $z_n$(の表す点)たちがどうなっていないとダメかを考えます。
候補をしぼった後は、具体的な例を使って、その値を本当にとり得るかをチェックしましょう。
解答編
問題
複素数の数列 $\{z_n\}$ に対する次の2つの条件を考える。
(i) すべての自然数 $n$ に対して、 $|z_n-z_{n+1}|=2^n$ が成り立つ。
(ii) すべての自然数 $n$ に対して、\[ \frac{(z_n-z_{n+1})(z_{n+2}-z_{n+3})}{ (z_{n+1}-z_{n+2})(z_{n+3}-z_{n}) } \] は実数である。
複素数の数列 $\{z_n\}$ で (i) と (ii) をともに満たすものをすべて考えたとき、\[ \frac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}} \]がとり得る値をすべて求めよ。
解答
複素数の数列 $\{z_n\}$ が (i) と (ii) をともに満たすとする。
(i)より、(ii)の分子は $0$ ではない。また、条件(ii)の式を変形すると
\begin{eqnarray}
& &
\frac{(z_{n}-z_{n+1})(z_{n+2}-z_{n+3})}{(z_{n+1}-z_{n+2})(z_{n+3}-z_{n})} \\[5pt]
&=&
\frac{z_{n+2}-z_{n+3}}{z_{n+1}-z_{n+2}} \cdot \frac{z_{n}-z_{n+1}}{z_{n+3}-z_{n}} \\[5pt]
&=&
\frac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}} \cdot \frac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}
\end{eqnarray}となる。これが実数であることは、 $\arg\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}} + \arg \dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}$ が $0$ または $\pi$ であることと同値である。
以下では、 $\mathrm{A}(z_{n}), \mathrm{B}(z_{n+1}), \mathrm{C}(z_{n+2}), \mathrm{D}(z_{n+3})$ とし、 $\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}$ が実数であることを示す。
もし、$\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}$ が実数でないなら、、$\dfrac{z_{n+1}-z_{n}}{z_{n+3}-z_{n}}$ も実数ではない。よって、3点 $\mathrm{B,C,D}$ は一直線上にはなく、3点 $\mathrm{B,A,D}$ も一直線上にはない。
また、(ii)より、 $\angle \mathrm{BCD}=\angle \mathrm{BAD}$ または $\angle \mathrm{BCD}+\angle \mathrm{DAB}=\pi$ が成り立つ(角度は反時計回りを正とし、等式は $2\pi$ の整数倍のズレを無視するものとする)。
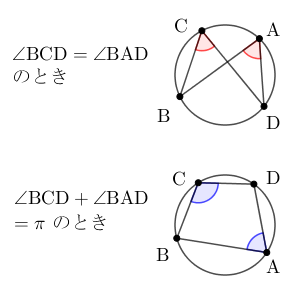
よって、いずれの場合も、4点 $\mathrm{A,B,C,D}$ は同一円周上にある。このことから、 $\mathrm{A}_n(z_n)$ とすると、 $\mathrm{A}_n$ は $\triangle\mathrm{A_1A_2A_3}$ の外接円上にあることになり、 $\mathrm{A}_n\mathrm{A}_{n+1}$ の長さはこの外接円の直径を超えることはない。一方、(i)より\[ \lim_{n\to\infty}|z_n-z_{n+1}|=\infty \]となるので、矛盾する。
以上から、$\dfrac{z_{n+3}-z_{n+2}}{z_{n+1}-z_{n+2}}$ が実数であることがわかる。これより、 $\mathrm{A}_{n+1}$, $\mathrm{A}_{n+2}$, $\mathrm{A}_{n+3}$ は同一直線上にあることがわかる。よって、$\mathrm{A}_n$ は直線 $\mathrm{A_1A_2}$ 上にあることがわかる。このとき、(ii)はつねに成り立つ。
$n=2021$ とすると、$\dfrac{z_{2024}-z_{2023}}{z_{2022}-z_{2023}}$ が実数だから、 $\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ も実数である。また
\begin{eqnarray}
\left|\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}\right|
&=&\dfrac{|z_{2022}-z_{2023}|}{|z_{2023}-z_{2024}|} \\[5pt]
&=&\dfrac{2^{2022}}{2^{2023}}
=\dfrac{1}{2} \\[5pt]
\end{eqnarray}なので、$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ がとる値の候補は $\pm\dfrac{1}{2}$ のみである。
ここで、 $z_n=2^n$ とすると、 $|z_n-z_{n+1}|=2^{n+1}-2^n=2^n$ より(i)を満たし、(ii)を満たすことは明らか。このとき
\begin{eqnarray}
\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}
&=&
\dfrac{2^{2022}-2^{2023}}{2^{2023}-2^{2024}} \\[5pt]
&=&
\dfrac{1-2}{2-2^2}=\frac{1}{2}
\end{eqnarray}となる。
また、 $z_n=\dfrac{(-2)^n}{3}$ とすると\[ |z_n-z_{n+1}|=\frac{\left| (-2)^n\{1-(-2)\}\right|}{3}=2^n \]より(i)を満たし、(ii)を満たすことは明らか。このとき
\begin{eqnarray}
\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}
&=&
\dfrac{3z_{2022}-3z_{2023}}{3z_{2023}-3z_{2024}} \\[5pt]
&=&
\dfrac{(-2)^{2022}-(-2)^{2023}}{(-2)^{2023}-(-2)^{2024}} \\[5pt]
&=&
\dfrac{1-(-2)}{(-2)-(-2)^2} \\[5pt]
&=&
\dfrac{3}{-6}
=
-\dfrac{1}{2} \\[5pt]
\end{eqnarray}となる。
以上から、$\dfrac{z_{2022}-z_{2023}}{z_{2023}-z_{2024}}$ がとりうる値は、 $\pm\dfrac{1}{2}$ である。(答)





