京都大学 理学部特色入試 2021年度 第4問 解説
(2020年11月に行われた特色入試の問題です。2021年に行われた特色入試の問題はこちら)
問題編
問題
$C$ を 1以上の実数、 $\{a_n\}$ を 0以上の整数からなる数列で $a_1=0$ 、 $a_2=1$ を満たすとする。 $xy$ 平面上の点 $\mathrm{A}_n=(a_n,a_{n+1})$ はすべての $n=1,2,3,\cdots$ について次の条件 (i), (ii), (iii) を満たすとする。
(i) 3点 $\mathrm{A}_n$, $\mathrm{O}$, $\mathrm{A}_{n+1}$ は同一直線上になく、三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ と三角形 $\mathrm{A}_{n+1}\mathrm{O}\mathrm{A}_{n+2}$ の内部は互いに交わらない。
(ii) 三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ の面積は $C$ より小さい。
(iii) $\angle\mathrm{A_1OA}_{n+1}\lt\dfrac{\pi}{4}$ かつ $\displaystyle \lim_{n\to\infty}\angle\mathrm{A_1OA}_{n+1}=\dfrac{\pi}{4}$ である。
ここで $\mathrm{O}$ は $xy$ 平面の原点を表す。以下の設問に答えよ。
(1) $C=100$ のとき、(i), (ii), (iii) を満たす数列 $\{a_n\}$ の例を1つ与えよ。
(2) 2以上の自然数 $n,m$ が $n\lt m$ を満たすとき、\[ 0\lt \dfrac{a_{n+1} }{a_n}-\dfrac{a_{m+1} }{a_m} \leqq 2C \left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \]となることを示せ。
(3) ある実数 $D$ が存在して、すべての自然数 $n$ について $a_{n+1}-a_n\leqq D$ となることを示せ。
(4) ある自然数 $n_0$ が存在して、点 $\mathrm{A}_{n_0},\mathrm{A}_{n_0+1},\mathrm{A}_{n_0+2},\cdots$ はすべて同一直線上にあることを示せ。
考え方
(1)は、シンプルな数列を使って、簡単に計算できるものを選びましょう。
(2)は、まず、面積を求めるために、点の位置関係を考えます。左側の不等式は、直線 $\mathrm{OA}_n$ の傾きがどんどん小さくなることを示せばいいです。右側の不等式は難しいですが、 $C$ が含まれているので、面積に関する条件から考えましょう。
$n$ と $m$ は離れているのでどういう関係かはよくわかりませんが、 $n$ と $n+1$ の場合なら調べやすいです。この場合をまず調べてから、 $n$ と $m$ の関係について考えましょう。
(3)は、まだあまり使っていない条件(iii)をどう利用するかを考えます。
(4)は、 $a_n$ が大きくなってくると、いろんな制約から、とれる値が限定されます。このことを利用して証明します。
見慣れない条件が多く考えづらいです。(2)は難しく、(4)もまた視点を変えて考えないといけないので大変です。
解答編
問題
$C$ を 1以上の実数、 $\{a_n\}$ を 0以上の整数からなる数列で $a_1=0$ 、 $a_2=1$ を満たすとする。 $xy$ 平面上の点 $\mathrm{A}_n=(a_n,a_{n+1})$ はすべての $n=1,2,3,\cdots$ について次の条件 (i), (ii), (iii) を満たすとする。
(i) 3点 $\mathrm{A}_n$, $\mathrm{O}$, $\mathrm{A}_{n+1}$ は同一直線上になく、三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ と三角形 $\mathrm{A}_{n+1}\mathrm{O}\mathrm{A}_{n+2}$ の内部は互いに交わらない。
(ii) 三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ の面積は $C$ より小さい。
(iii) $\angle\mathrm{A_1OA}_{n+1}\lt\dfrac{\pi}{4}$ かつ $\displaystyle \lim_{n\to\infty}\angle\mathrm{A_1OA}_{n+1}=\dfrac{\pi}{4}$ である。
ここで $\mathrm{O}$ は $xy$ 平面の原点を表す。以下の設問に答えよ。
(1) $C=100$ のとき、(i), (ii), (iii) を満たす数列 $\{a_n\}$ の例を1つ与えよ。
解答
(1) $a_n=n-1$ が条件を満たすことを示す。
直線 $\mathrm{OA}_{n+1}$ は、$y=\dfrac{a_{n+2} }{a_{n+1} }x=\left(1+\dfrac{1}{n}\right)x$ と表すことができる。 $x=n-1$ とすると\[ \left(1+\dfrac{1}{n}\right)(n-1)\lt n \]であり、 $x=n+1$ とすると\[\left(1+\dfrac{1}{n}\right)(n+1) \gt n+2 \]なので、直線 $\mathrm{OA}_{n+1}$ について、点 $\mathrm{A}_n(n-1,n)$ と点 $\mathrm{A}_{n+2}(n+1,n+2)$ は異なる側にある。よって、条件(i)を満たすことがわかる。
直線 $\mathrm{OA}_{n+1}$ の傾き $\dfrac{n+1}{n}$ は $1$ より大きく、 $n\to \infty$ のとき $1$ に収束するので、条件(iii) を満たすこともわかる。
最後に、三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ の面積を求める。
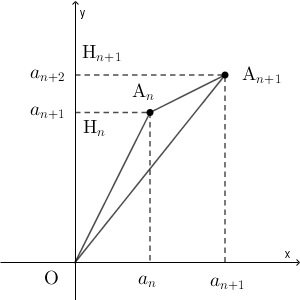
点 $\mathrm{A}_{n}$ から $y$ 軸に下した垂線の足を $\mathrm{H}_{n}$ とすると、三角形 $\mathrm{A}_{n+1}\mathrm{O}\mathrm{H}_{n+1}$ から、三角形 $\mathrm{A}_{n}\mathrm{O}\mathrm{H}_{n}$ と台形 $\mathrm{A}_{n+1}\mathrm{A}_{n}\mathrm{H}_{n}\mathrm{H}_{n+1}$ の面積を引けばいいので
\begin{eqnarray}
& &
\frac{n(n+1)}{2}-\frac{(n-1)n}{2}-\frac{\{(n-1)+n\}\cdot 1}{2} \\[5pt]
&=&
\frac{n^2+n}{2}-\frac{n^2-n}{2}-\frac{2n-1}{2} \\[5pt]
&=&
\frac{1}{2} \\[5pt]
\end{eqnarray}となる。よって、面積は $C=100$ より小さい。
以上から、 $a_n=n-1$ とすると数列 $\{a_n\}$ が条件(i)(ii)(iii)を満たすことがわかる。
(1)終
解答編 つづき
(2) 2以上の自然数 $n,m$ が $n\lt m$ を満たすとき、\[ 0\lt \dfrac{a_{n+1} }{a_n}-\dfrac{a_{m+1} }{a_m} \leqq 2C \left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \]となることを示せ。
解答
(2)
条件(iii)より、直線 $\mathrm{OA}_{n+1}$ の傾きは1より大きいので、 $a_{n+2}\gt a_{n+1}$ となる。よって、数列 $\{a_n\}$ は狭義単調増加である。
また、条件(i)より、直線 $\mathrm{OA}_{n+1}$ について、 $\mathrm{A}_{n}$ と $\mathrm{A}_{n+2}$ は異なる側にある。直線 $\mathrm{OA}_{3}$ の傾きは $\mathrm{OA}_2$ の傾きより小さいので、数学的帰納法から、直線 $\mathrm{OA}_2$, $\mathrm{OA}_3$, $\mathrm{OA}_4,\cdots$ の傾きは、狭義単調減少である。なので、 $2\leqq n\lt m$ のとき、\[ 0\lt \frac{a_{n+1} }{a_n}-\frac{a_{m+1} }{a_m} \quad\cdots(*1) \]が成り立つ。
ここまでの内容から、点 $\mathrm{A}_{n+1}$ は、直線 $y=x$ より上にあり、直線 $\mathrm{OA}_n$ より下(点 $(1,0)$ を含む側)にあるので、次のような位置関係にある。((1)と同様に、点 $\mathrm{A}_{n}$ から $y$ 軸に下した垂線の足を $\mathrm{H}_{n}$ としている。)

これより、三角形 $\mathrm{A}_n\mathrm{O}\mathrm{A}_{n+1}$ の面積は
\begin{eqnarray}
& &
\frac{a_{n+1}a_{n+2} }{2}-\frac{a_n a_{n+1} }{2} -\frac{(a_n+a_{n+1})(a_{n+2}-a_{n+1})}{2} \\[5pt]
&=&
\frac{a_{n+1}a_{n+2} -a_n a_{n+1} }{2} \\
& &-\frac{a_na_{n+2}-a_na_{n+1}+a_{n+1}a_{n+2}-a_{n+1}a_{n+1} }{2} \\[5pt]
&=&
\frac{a_{n+1}^2-a_na_{n+2} }{2} \\[5pt]
\end{eqnarray}となる。よって、条件(ii)より\[ a_{n+1}^2-a_na_{n+2}\lt 2C \]が成り立つ。
ここで、 $k$ を2以上の自然数とするとき
\begin{eqnarray}
& &
\frac{a_{k+1} }{a_k} -\frac{a_{k+2} }{a_{k+1} } \\[5pt]
&=&
\frac{a_{k+1}^2-a_ka_{k+2} }{a_ka_{k+1} } \\[5pt]
&\lt&
\frac{2C}{a_ka_{k+1} } \\[5pt]
&=&
2C \left(\frac{1}{a_k}-\frac{1}{a_{k+1} }\right)\cdot\frac{1}{a_{k+1}-a_k} \\[5pt]
&\leqq&
2C \left(\frac{1}{a_k}-\frac{1}{a_{k+1} }\right) \\[5pt]
\end{eqnarray}が成り立つ。なお、最後は、数列 $\{a_n\}$ が狭義単調増加であり、整数の値をとることを用いている。
ここで、 $k=n,n+1,\cdots, m-1$ として辺々足すと
\begin{eqnarray}
\sum_{k=n}^{m-1} \left(\frac{a_{k+1} }{a_k} -\frac{a_{k+2} }{a_{k+1} }\right) \leqq \sum_{k=n}^{m-1} 2C \left(\frac{1}{a_k}-\frac{1}{a_{k+1} }\right)
\\[5pt]
\frac{a_{n+1} }{a_n} -\frac{a_{m+1} }{a_m} \leqq 2C \left(\frac{1}{a_n}-\frac{1}{a_m}\right) \quad \cdots (*2) \\[5pt]
\end{eqnarray}となる。
(*1)(*2)より、2以上の自然数 $n,m$ が $n\lt m$ を満たすとき、\[ 0\lt \dfrac{a_{n+1} }{a_n}-\dfrac{a_{m+1} }{a_m} \leqq 2C \left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \]となる。
(2)終
解答編 つづき
(3) ある実数 $D$ が存在して、すべての自然数 $n$ について $a_{n+1}-a_n\leqq D$ となることを示せ。
解答
(3)
(2)より $2\leqq n\lt m$ のとき、
\begin{eqnarray}
& &
\dfrac{a_{n+1} }{a_n}-\dfrac{a_{m+1} }{a_m} \leqq 2C \left(\dfrac{1}{a_n}-\dfrac{1}{a_m}\right) \leqq \dfrac{2C}{a_n} \\[5pt]
& &
\dfrac{a_{n+1} }{a_n}-1 \leqq \dfrac{a_{m+1} }{a_m}-1+\dfrac{2C}{a_n} \\[5pt]
& &
a_{n+1}-a_n \leqq \left(\dfrac{a_{m+1} }{a_m}-1\right)a_n+2C \\[5pt]
\end{eqnarray}が成り立つ。ここで $m$ は $n$ より大きな自然数であれば何でもよく、\[ \lim_{m\to\infty} \frac{a_{m+1} }{a_m}=1 \]が成り立つ(条件(iii)より)ので、 $m\to\infty$ とすると
\begin{eqnarray}
a_{n+1}-a_n \leqq 2C \\[5pt]
\end{eqnarray}が成り立つ。 $n=1$ のときもこれは成り立つので、 $D=2C$ とすれば、すべての自然数 $n$ について $a_{n+1}-a_n\leqq D$ となる。
(3)終
解答編 つづき
(4) ある自然数 $n_0$ が存在して、点 $\mathrm{A}_{n_0},\mathrm{A}_{n_0+1},\mathrm{A}_{n_0+2},\cdots$ はすべて同一直線上にあることを示せ。
解答
(4)
数列 $\{a_n\}$ は狭義単調増加なので、 $n\geqq n_0$ ならば $a_n\gt (2C)^2$ となるような $n_0$ が存在する。なお、このとき、 $a_n\gt 2C$ も成り立つ。
$n\geqq n_0$ とし、 $a_{n+1}-a_n=K$ とする。(3)より、 $K\leqq 2C$ である。面積に関する条件(ii)から\[ 0\lt a_{n+1}^2-a_na_{n+2}\lt 2C \]が成り立つ。右側の不等式から\[ \frac{a_{n+1}^2-2C}{a_n}\lt a_{n+2} \]となり、左側の不等式から\[ a_{n+2}\lt\frac{a_{n+1}^2}{a_{n} } \]となる。よって
\begin{eqnarray}
& &
\frac{a_{n+1}^2-2C}{a_n}\lt a_{n+2} \lt\frac{a_{n+1}^2}{a_n} \\[5pt]
& &
\frac{(a_n+K)^2-2C}{a_n}\lt a_{n+2} \lt\frac{(a_n+K)^2}{a_n} \\[5pt]
& &
a_n+2K+\frac{K^2-2C}{a_n}\lt a_{n+2} \lt a_n+2K+\frac{K^2}{a_n} \\[5pt]
\end{eqnarray}ここで、 $a_{n+1}=a_n+K$ を辺々引くと
\begin{eqnarray}
& &
K+\frac{K^2-2C}{a_n}\lt a_{n+2}-a_{n+1} \lt K+\frac{K^2}{a_n} \\[5pt]
\end{eqnarray}$n_0$ の決め方から、一番右側の式は\[ K+\frac{K^2}{a_n}\leqq K+\frac{(2C)^2}{a_n}\lt K+1 \]となり、一番左側の式は\[ K+\frac{K^2-2C}{a_n}\gt K-\frac{2C}{a_n}\gt K-1 \]となる。 $a_{n+2}-a_{n+1}$ は整数なので、 $a_{n+2}-a_{n+1}=K$ となる。
以上から、 $a_{n_0+1}-a_{n_0}=K$ とすると、 $n\geqq n_0$ ならば $a_{n+1}-a_n=K$ となることがわかる。なので、 $n\geqq n_0$ ならば直線 $\mathrm{A}_n\mathrm{A}_{n+1}$ の傾きは\[ \frac{a_{n+2}-a_{n+1} }{a_{n+1}-a_n}=1 \]で一定であるので、点 $\mathrm{A}_{n_0},\mathrm{A}_{n_0+1},\mathrm{A}_{n_0+2},\cdots$ はすべて同一直線上にあることが示せた。
(4)終





