京都大学 理学部特色入試 2021年度 第2問 解説

（2020年11月に行われた特色入試の問題です。2021年に行われた特色入試の問題はこちら）

問題編

問題

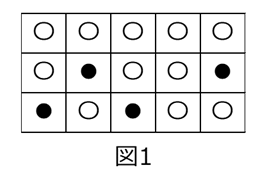
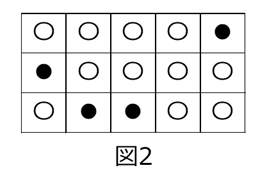
　自然数 $n,m$ に対して横 $n$ 個、縦 $m$ 個からなる $n\times m$ 個のマスを考え、それぞれのマスに1つずつ白玉または黒玉を入れる。その白玉と黒玉の入れ方のうち、黒玉が上下左右いずれにも隣り合わないような入れ方の総数を $a_{n,m}$ とする。例えば $n=5,m=3$ のとき、図1の入れ方は黒玉が上下左右いずれにも隣り合わないような入れ方であり、図2の入れ方は黒玉が左右に隣り合っている入れ方である。

下の設問に答えよ。

(1) $a_{n,2}$ を求めよ。

(2) ある正の実数 $D$ が存在して、すべての自然数 $n$ について\[ \frac{1}{2} \leqq \frac{\log_2 a_{n,n} }{n^2} \leqq \frac{1}{2}\log_2(1+\sqrt{2})+\frac{D}{n} \]となることを示せ。

考え方

(1)はよくある数列の問題です。普通の大学入試であれば、これだけでも十分難しいですが、特色入試の場合では、これは解けないとダメでしょう。

(2)は、 $a_{n,n}$ の具体的な値は求めなくてもいいことに注意しましょう。条件より厳しい入れ方や緩い入れ方を考えて、数えやすいもので評価していきます。

左側は、より厳しい入れ方、限定的な入れ方を考えます。式変形で攻めるのではなく、わかりやすい入れ方を考えるようにします。

右側の式にある $1+\sqrt{2}$ がどこから湧いて出てくるのか、パッと見た感じでは謎ですが、(1)を解けば意味は分かるでしょう。これで、(2)では(1)を使いそうだというのはわかりますが、使い方は少し考えないといけません。

---

解答編

問題

　自然数 $n,m$ に対して横 $n$ 個、縦 $m$ 個からなる $n\times m$ 個のマスを考え、それぞれのマスに1つずつ白玉または黒玉を入れる。その白玉と黒玉の入れ方のうち、黒玉が上下左右いずれにも隣り合わないような入れ方の総数を $a_{n,m}$ とする。例えば $n=5,m=3$ のとき、図1の入れ方は黒玉が上下左右いずれにも隣り合わないような入れ方であり、図2の入れ方は黒玉が左右に隣り合っている入れ方である。

下の設問に答えよ。

(1) $a_{n,2}$ を求めよ。

解答

(1)
横 $n$ 列、縦 $2$ 列のときに、条件を満たす玉の入れ方のうち、右端が上から白白となっている場合の数を $b_n$ とする。同様に、白黒は $c_n$ 、黒白は $d_n$ とする。黒黒の場合は条件を満たさない。

$n=1$ のときは、 $b_1=1$, $c_1=1$, $d_1=1$ である。

$n=k+1$ のとき、左から $k$ 列目が上から白白となっている場合、右端は、白白、白黒、黒白のどの場合もあり得る。

左から $k$ 列目が上から白黒となっている場合、右端は、白白、黒白の場合がある。

左から $k$ 列目が上から黒白となっている場合、右端は、白白、白黒の場合がある。

以上から、 $n=k+1$ と $n=k$ のときを比べると、次の3つの関係式が成り立つ。
\begin{eqnarray} b_{k+1} &=& b_k+c_k+d_k \\[5pt] c_{k+1} &=& b_k +d_k \\[5pt] d_{k+1} &=& b_k+c_k \\[5pt] \end{eqnarray}$e_k=c_k+d_k$ とすると、上の3つの関係式から、次の2つの関係式が導ける。 \begin{eqnarray} b_{k+1} &=& b_k+e_k \\[5pt] e_{k+1} &=& 2b_k +e_k \\[5pt] \end{eqnarray}

ここで、\[ b_{k+1}-xe_{k+1}=y(b_k-xe_k) \]とおくと
\begin{eqnarray} b_k+e_k -x(2b_k+e_k) &=& yb_k -xye_k \\[5pt] (1-2x)b_k +(1-x)e_k &=& yb_k -xye_k \\[5pt] \end{eqnarray}なので、\[ 1-2x=y,\ 1-x=-xy \]なら成り立つ。1つ目の式を2つ目に代入して \begin{eqnarray} 1-x &=& -x(1-2x) \\[5pt] 2x^2 &=& 1 \\[5pt] x &=& \pm\frac{1}{\sqrt{2} } \\[5pt] \end{eqnarray}が得られる。 $y=1-2x$ なので、 $y=1\mp\sqrt{2}$ となる（複合同順）。

よって、次の2つの式が成り立つ。
\begin{eqnarray} b_{k+1}-\frac{1}{\sqrt{2} }e_{k+1} &=& (1-\sqrt{2}) \left(b_k-\frac{1}{\sqrt{2} }e_k\right) \\[5pt] b_{k+1}+\frac{1}{\sqrt{2} }e_{k+1} &=& (1+\sqrt{2}) \left(b_k+\frac{1}{\sqrt{2} }e_k\right) \\[5pt] \end{eqnarray}ここで、 $b_1=1$, $e_1=c_1+d_1=2$ なので、次の2つの式が成り立つ。 \begin{eqnarray} b_k-\frac{1}{\sqrt{2} }e_k &=& (1-\sqrt{2})^{k-1} (1-\sqrt{2})= (1-\sqrt{2})^k \\[5pt] b_k+\frac{1}{\sqrt{2} }e_k &=& (1+\sqrt{2})^{k-1} (1+\sqrt{2})= (1+\sqrt{2})^k \\[5pt] \end{eqnarray}これらから \begin{eqnarray} b_k &=& \frac{(1+\sqrt{2})^k+(1-\sqrt{2})^k}{2} \\[5pt] e_k &=& \sqrt{2}\cdot \frac{(1+\sqrt{2})^k-(1-\sqrt{2})^k}{2} \\[5pt] \end{eqnarray}が得られる。

以上より
\begin{eqnarray} a_{n,2} &=& b_n+e_n \\[5pt] &=& \frac{ (1+\sqrt{2})^n+(1-\sqrt{2})^n +\sqrt{2}\{ (1+\sqrt{2})^n-(1-\sqrt{2})^n \} }{2} \\[5pt] &=& \frac{ (1+\sqrt{2})^{n+1}+(1-\sqrt{2})^{n+1} }{2} \\[5pt] \end{eqnarray}と求められる。

(1)終

解答編 つづき

(2) ある正の実数 $D$ が存在して、すべての自然数 $n$ について\[ \frac{1}{2} \leqq \frac{\log_2 a_{n,n} }{n^2} \leqq \frac{1}{2}\log_2(1+\sqrt{2})+\frac{D}{n} \]となることを示せ。

解答

(2)
左上を基準とし、左から $i$ 番目、上から $j$ 番目のマスを、 $(i,j)$ で表すことにする。このとき、 $i+j$ が偶数になるマス $(i,j)$ について考える（下の図のグレーの部分）。

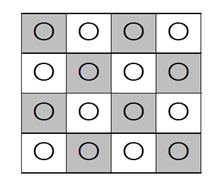
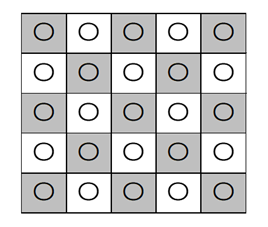
$i+j$ が偶数となるマス $(i,j)$ に、それぞれ黒玉か白玉を入れ、奇数となるマスには白玉を入れると、黒玉は必ず隣り合わないような入れ方となる。 $i+j$ が偶数になるマスの個数は、 $n$ が偶数のときは $\dfrac{n^2}{2}$ 個であり、奇数のときは $\dfrac{n^2+1}{2}$ なので、必ず $\dfrac{n^2}{2}$ 以上である。よって、 $a_{n,n}$ は、 $2$ の $\dfrac{n^2}{2}$ 乗以上となる。このことから
\begin{eqnarray} & & \frac{n^2}{2} \leqq \log_2 a_{n,n} \\[5pt] & & \frac{1}{2} \leqq \frac{\log_2 a_{n,n} }{n^2} \quad\cdots(*1) \\[5pt] \end{eqnarray}が成り立つ。

次に、このマスを、上から2行ずつ切っていくことにする。 $n$ が奇数の場合は、すべて白玉を入れた行を追加し、これを $n+1$ 行目と考える。こうすると、 $n$ が偶数の場合は、2行ずつのエリアが $\dfrac{n}{2}$ 個でき、 $n$ が奇数の場合は $\dfrac{n+1}{2}$ 個できる。いずれにしても、 $\dfrac{n+1}{2}$ を超えることはない。

このとき、それぞれのどの2行を見ても、「黒玉が隣り合わない入れ方」になっている。そのため、 $a_{n,n}$ は $a_{n,2}$ の $\dfrac{n+1}{2}$ 乗を超えることはない。よって、
\begin{eqnarray} & & \log_2 a_{n,n} \\[5pt] &\leqq & \frac{n+1}{2}\log_2 a_{n,2} \\[5pt] &=& \frac{n+1}{2}\log_2 \frac{ (1+\sqrt{2})^{n+1}+(1-\sqrt{2})^{n+1} }{2} \\[5pt] &\leqq& \frac{n+1}{2}\log_2 (1+\sqrt{2})^{n+1} \\[5pt] &=& \frac{(n+1)^2}{2}\log_2 (1+\sqrt{2}) \\[5pt] &=& \frac{n^2}{2}\log_2 (1+\sqrt{2})+ \left(n+\frac{1}{2}\right)\log_2 (1+\sqrt{2}) \\[5pt] &\leqq & \frac{n^2}{2}\log_2 (1+\sqrt{2})+ (n+n)\log_2 (1+3) \\[5pt] &\leqq & \frac{n^2}{2}\log_2 (1+\sqrt{2})+ 4n \\[5pt] \end{eqnarray}となる。これより、\[ \log_2 a_{n,n} \leqq \frac{n^2}{2}\log_2 (1+\sqrt{2})+ 4n \]だから\[ \frac{\log_2 a_{n,n} }{n^2} \leqq \frac{1}{2}\log_2(1+\sqrt{2})+\frac{4}{n} \quad\cdots(*2) \]が成り立つ。

(*1)(*2)より、 $D=4$ とすれば、すべての自然数 $n$ について\[ \frac{1}{2} \leqq \frac{\log_2 a_{n,n} }{n^2} \leqq \frac{1}{2}\log_2(1+\sqrt{2})+\frac{D}{n} \]が成り立つ。

(2)終

解説

(1)は、 $k$ 番目と $k+1$ 番目の関係から漸化式を作る、という典型的な流れです。漸化式を解くのは少し大変ですが、計算間違いに注意して解きましょう。

(2)は、左側の不等式を変形すると\[ 2^{n^2/2}\leqq a_{n,n} \]となります。ここで、 $2^{n^2/2}$ とは、 $n^2$ の半分のマスについて、白か黒か選べる、と考えれば、上のように市松模様を使えばいいことがわかります。

右側の不等式は、右辺に $(1+\sqrt{2})$ があり、これが(1)の答えに出てきているので、これを使うんだろう、と目星をつけて考えます。全体で「黒玉が隣り合わない」ので、2行ずつ区切っても各エリアで「黒玉が隣り合わない」ことが決まっているので、(1)の結果を使って評価します。 $D$ は誤差の部分を適当に評価すればOKです。