京都大学 理学部特色入試 2021年度 第1問 解説

（2020年11月に行われた特色入試の問題です。2021年に行われた特色入試の問題はこちら）

問題編

問題

　$n$ を 3以上の自然数、 $\lambda$ を実数とする。次の条件(i),(ii) を満たす空間ベクトル $\vec{v_1},\vec{v_2},\cdots ,\vec{v_n}$ が存在するための $n$ と $\lambda$ が満たすべき条件を求めよ。

　(i) $\vec{v_1},\vec{v_2},\cdots ,\vec{v_n}$ は相異なる長さ 1 の空間ベクトルである。

　(ii) $i\ne j$ のときベクトル $\vec{v_i}$ と $\vec{v_j}$ の内積は $\lambda$ に等しい。

考え方

いろいろ実験してみると、答えをある程度予想できるかもしれませんが、きちんと示すにはかなり面倒です。図形の性質も利用して示すことを考えましょう。

---

解答編

問題

　$n$ を 3以上の自然数、 $\lambda$ を実数とする。次の条件(i),(ii) を満たす空間ベクトル $\vec{v_1},\vec{v_2},\cdots ,\vec{v_n}$ が存在するための $n$ と $\lambda$ が満たすべき条件を求めよ。

　(i) $\vec{v_1},\vec{v_2},\cdots ,\vec{v_n}$ は相異なる長さ 1 の空間ベクトルである。

　(ii) $i\ne j$ のときベクトル $\vec{v_i}$ と $\vec{v_j}$ の内積は $\lambda$ に等しい。

解答

空間ベクトル $\vec{v_1},\vec{v_2},\cdots ,\vec{v_n}$ が条件を満たすとする。

$\mathrm{A}_i$ の位置ベクトルが $\vec{v_i}$ となるように点 $\mathrm{A}_i$ をとる。原点を中心とする半径 1 の球の表面を $S$ とすると、(i)より、 $\mathrm{A}_i$ は $S$ 上の点であり、 $i\ne j$ ならば $\mathrm{A}_i$ と $\mathrm{A}_j$ は異なる点である。

(ii)より、 $i\ne j$ のときは $\cos\angle\mathrm{A}_i\mathrm{O}\mathrm{A}_j=\lambda$ なので、ある $\theta$ $(0\leqq \theta\leqq \pi)$ が存在して

　$i\ne j$ のとき $\angle\mathrm{A}_i\mathrm{O}\mathrm{A}_j=\theta$

とできる。ここで、点 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$ は相異なる点なので、 $\theta\ne 0,\pi$ であるから、 $0\lt \theta \lt\pi$ として考える。

回転することにより、 $\mathrm{A}_1$, $\mathrm{A}_2$ の座標を、それぞれ、 $(1,0,0)$, $(\cos\theta,\sin\theta,0)$ としても一般性を失わない。

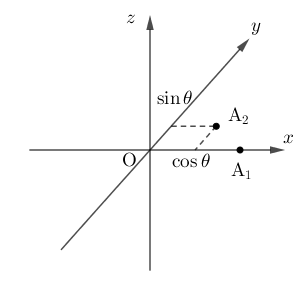
$i\geqq 2$ のとき、 $\mathrm{A}_i$ から $x$ 軸に下した垂線の足を $\mathrm{H}$ とすると、 $\angle\mathrm{A_1OA}_i=\theta$ なので、 $\mathrm{H}$ の座標は $(\cos\theta,0,0)$ である。よって、 $i\geqq 2$ のとき、 $\mathrm{A}_i$ は、 $\mathrm{A}_2$ を通る $x$ 軸に垂直な平面で、球の表面 $S$ を切ったときの断面上にあることがわかる。この断面を $C$ とおく。この断面 $C$ は円の円周であり、中心は $x$ 軸上にある。

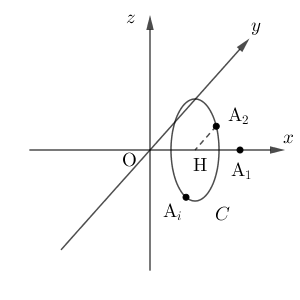
よって、条件を満たす空間ベクトルが存在するなら、 $i\geqq 2$ のとき $\mathrm{A}_i$ は円 $C$ 上にある。

以下では、 $0\lt \theta\lt\pi$ として、 $\mathrm{A}_1(1,0,0)$, $\mathrm{A}_2(\cos\theta,\sin\theta,0)$ とし、条件を満たすように $\mathrm{A_3},\mathrm{A_4},\cdots$ を円 $C$ 上にとれるかどうかを、 $n$ の値で場合分けをして考えていく。

(a) $n=3$ のとき

断面 $C$ 上の点 $\mathrm{P}$ について考えると、 $\angle\mathrm{A_1OP}=\theta$ である。よって、 $\angle\mathrm{A_2OP}=\theta$ となるように点 $\mathrm{P}$ がとれるかどうかを考える。

$\angle\mathrm{A_2OP}$ の最小値は $0$ である。最大となるのは、余弦定理から線分 $\mathrm{A_2P}$ が最大になるときだとわかるので、 $\mathrm{A_2P}$ が断面 $C$ の直径のときである。このとき、 $\mathrm{P}$ の座標は $(\cos\theta,-\sin\theta,0)$ である。

$0\lt \theta\leqq \dfrac{\pi}{2}$ のとき、 $\mathrm{A_2P}$ が円 $C$ の直径なら、 $\angle\mathrm{A_2OP}=2\theta$ となる。

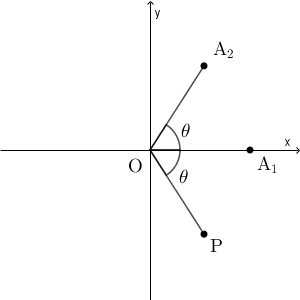
$\angle\mathrm{A_2OP}$ は $0$ から $2\theta$ までのすべての値をとりうるので、 $\angle\mathrm{A_2OA_3}=\theta$ を満たすように $\mathrm{A_3}$ をとることができる。

$\dfrac{\pi}{2}\lt \theta\leqq \pi$ のとき、 $\mathrm{A_2P}$ が円 $C$ の直径なら、 $\angle\mathrm{A_2OP}=2\pi-2\theta$ となる。

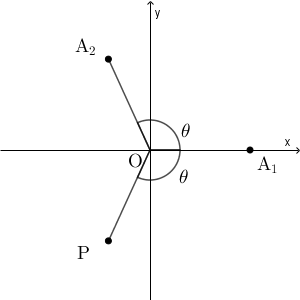
$\angle\mathrm{A_2OP}$ は $0$ から $2\pi-2\theta$ までのすべての値をとりうる。ここで、 $\theta\leqq 2\pi-2\theta$ とすると $\theta\leqq\dfrac{2}{3}\pi$ なので、 $\dfrac{\pi}{2}\lt \theta\leqq \dfrac{2}{3}\pi$ のときは $\angle\mathrm{A_2OA_3}=\theta$ を満たすように $\mathrm{A_3}$ をとることができる。これ以外の場合は、 $\angle\mathrm{A_2OA_3}=\theta$ を満たす $\mathrm{A_3}$ は存在しない。

以上から、 $n=3$ のときは、条件を満たす空間ベクトルが存在することは、 $0\lt\theta\leqq \dfrac{2}{3}\pi$ を満たすこと、つまり、 $-\dfrac{1}{2}\leqq \lambda\lt 1$ を満たすことと同値である。

(b) $n=4$ のとき

まずは、条件を満たす空間ベクトルが存在すると仮定して考える。

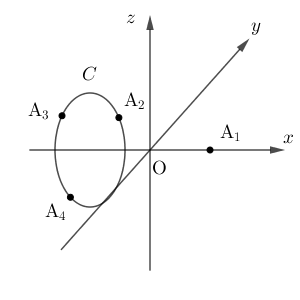
$\mathrm{O},\mathrm{A_2},\mathrm{A_3}$ を含む平面と断面 $C$ は2点でしか交わらないので、 $\mathrm{A_4}$ はこの平面上にはない。よって、\[ \vec{v_1}=p\vec{v_2}+q\vec{v_3}+r\vec{v_4} \]を満たす実数 $p,q,r$ が存在する。このとき、このベクトルと、 $\vec{v_1}$, $\vec{v_2}$, $\vec{v_3}$, $\vec{v_4}$ との内積をそれぞれ計算すると、
\begin{eqnarray} 1 &=& p\lambda +q\lambda +r\lambda \\[5pt] \lambda &=& p +q\lambda +r\lambda \\[5pt] \lambda &=& p\lambda +q +r\lambda \\[5pt] \lambda &=& p\lambda +q\lambda +r \\[5pt] \end{eqnarray}という4つの式が得られる。1つ目の式から\[ p+q+r=\frac{1}{\lambda} \]となる。2つ目から4つ目の式を辺々加えると \begin{eqnarray} 3\lambda &=& (1+2\lambda)(p+q+r) \\[5pt] 3\lambda^2 &=& 1+2\lambda \\[5pt] 3\lambda^2-2\lambda-1 &=& 0 \\[5pt] (3\lambda+1)(\lambda-1) &=& 0 \\[5pt] \end{eqnarray}となる。これより、条件を満たすものがあるとすれば、 $\lambda=-\dfrac{1}{3}$ である。

以下では、 $\lambda=-\dfrac{1}{3}$ のときに条件をみたす空間ベクトルが存在することを示す。

このとき、 $\mathrm{A_2}$ の座標は $\left(-\dfrac{1}{3},\dfrac{2\sqrt{2} }{3},0\right)$ であり、断面 $C$ の半径は $\dfrac{2\sqrt{2} }{3}$ である。ここで、 $\triangle\mathrm{A_2A_3A_4}$ が正三角形となるように、断面 $C$ 上に点 $\mathrm{A_3,A_4}$ をとると、この正三角形の一辺の長さは $\dfrac{2\sqrt{6} }{3}$ である。また、
\begin{eqnarray} \mathrm{A_1A_2}^2 &=& 1^2+1^2-2\cdot1\cdot1\cdot\left(-\dfrac{1}{3}\right) \\[5pt] &=& 2+\dfrac{2}{3} = \dfrac{8}{3} \\[5pt] \end{eqnarray}なので、 $\mathrm{A_1A_2}=\dfrac{2\sqrt{6} }{3}$ である。同様にして $\mathrm{A_1A_2}=\mathrm{A_1A_3}=\mathrm{A_1A_4}$ となることがわかり、これは正三角形 $\mathrm{A_2A_3A_4}$ の一辺の長さとも等しい。よって、 $i\ne j$ のとき \begin{eqnarray} |\vec{v_i}-\vec{v_j}|^2 &=& 2-2\vec{v_i}\cdot\vec{v_j} \\[5pt] \vec{v_i}\cdot\vec{v_j} &=& 1-\frac{1}{2}\cdot\left(\dfrac{2\sqrt{6} }{3}\right)^2=-\frac{1}{3}=\lambda \\[5pt] \end{eqnarray}となる。よって、上のように $\mathrm{A_3},\mathrm{A_4}$ をとれば、空間ベクトル $\vec{v_1}$, $\vec{v_2}$, $\vec{v_3}$, $\vec{v_4}$ は条件をみたすことがわかる。（なお、このとき、四面体 $\mathrm{A_1A_2A_3A_4}$ は正四面体である。）

(c) $n\geqq 5$ のとき

条件を満たす空間ベクトルがあるとすると、 $i\ne j$ のときに
\begin{eqnarray} |\overrightarrow{ \mathrm{ A_i A_j } }|^2 &=& |v_j-v_i|^2 \\[5pt] &=& 1-2\lambda+1=2-2\lambda \end{eqnarray}となる。よって、三角形 $\mathrm{A_2A_3A_4}$ も三角形 $\mathrm{A_2A_3A_5}$ も正三角形となる。しかし、 $\mathrm{A_2,A_3,A_4,A_5}$ は円 $C$ 上にあり、 $\mathrm{A_4,A_5}$ は異なる点なので、どちらも正三角形になることはない。

よって、このときは条件を満たす空間ベクトルは存在しない。

(a)から(c)より、条件を満たす空間ベクトルが存在するための条件は

　「 $n=3$ かつ $-\dfrac{1}{2}\leqq \lambda \lt 1$ 」
　　または
　「 $n=4$ かつ $\lambda=-\dfrac{1}{3}$ 」

となる。（終）