京都大学 理系 2016年度 第4問 解説
問題編
【問題】
xyz空間において、平面$y=z$の中で\[ |x|\leqq \frac{e^y+e^{-y} }{2}-1, \quad 0\leqq y \leqq \log a \]で与えられる図形Dを考える。ただしaは1より大きい定数とする。
この図形Dをy軸のまわりに1回転させてできる立体の体積を求めよ。
【考え方】
図を考えるのが大変ですが、最終的にy軸のまわりで1回転するので、y軸で切って考えてみるのがいいですね。すると、回転体の断面は輪のような形になるのがわかります。
断面の面積は2つの円の面積の差で出せます。あとはそれを積分すれば、求めたい体積が得られます。
解答編
【問題】
xyz空間において、平面$y=z$の中で\[ |x|\leqq \frac{e^y+e^{-y} }{2}-1, \quad 0\leqq y \leqq \log a \]で与えられる図形Dを考える。ただしaは1より大きい定数とする。
この図形Dをy軸のまわりに1回転させてできる立体の体積を求めよ。
【解答】
$0 \leqq k \leqq \log a$とする。図形Dを$y=k$で切断した断面図は、次のようになる。
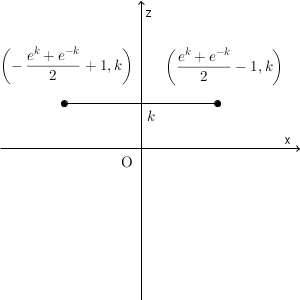
ここで、\[ \frac{e^k+e^{-k} }{2}-1 = \frac{ ( e^{\frac{k}{2} } -e^{\frac{-k}{2} } )^2 }{2} \geqq 0 \]である。
また、この線分の中で、原点から一番近い点は、原点からk離れており、一番遠い点は原点から\[\sqrt{ k^2 + \left( \frac{e^k+e^{-k} }{2}-1 \right)^2 }\]離れている。
回転体を$y=k$で切断した断面図は、次の図の色のついた部分のようになる。

この断面の面積は、線分の中で原点から一番近い点、遠い点との距離より、
\begin{eqnarray}
& & \pi \left\{k^2 + \left( \frac{e^k+e^{-k} }{2}-1 \right)^2\right\} - \pi k^2 \\[5pt]
&=& \pi \left( \frac{e^k+e^{-k} }{2}-1 \right)^2
\end{eqnarray}である。
よって、求める体積は、
\begin{eqnarray}
& & \pi \int_0^{\log a} \left( \frac{e^y+e^{-y} }{2}-1 \right)^2 dy \\[5pt]
&=& \pi \int_0^{\log a} \frac{e^{2y}+e^{-2y}+4 +2 -4e^y-4e^{-y} }{4} dy \\[5pt]
&=& \pi \left[ \frac{e^{2y} }{8} -\frac{e^{-2y} }{8} +\frac{3y}{2} -e^y +e^{-y} \right]_0^{\log a} \\[5pt]
&=& \pi \left( \frac{a^2}{8} -\frac{1}{8} -\frac{a^{-2} }{8} +\frac{1}{8} +\frac{3\log a}{2} -a +1 +a^{-1} -1 \right) \\[5pt]
&=& \pi \left( \frac{a^2}{8} -\frac{1}{8a^2} +\frac{3\log a}{2} -a +\frac{1}{a} \right)
\end{eqnarray}となる。
【解答終】
【解説】
途中で$\frac{e^k+e^{-k} }{2}-1 \geqq 0$であることに言及していますが、これは図形Dの断面の線分がマイナスになっていないことを確かめています。もしマイナスになることがあれば、断面が存在しないことになるので、積分するときにその区間を除く必要が出てきます。
斜めの平面上にある図形を回転するので、どういうものが出来上がるのか想像しにくいです。こういうときは、はじめから断面で考えた方がいいです。いきなり3次元で考えるより、2次元に落として考えたほうが、解きやすいと思います。





