京都大学 理系 2006年度 第5問 解説
問題編
【問題】
$\triangle \mathrm{ ABC }$に対し、辺AB上に点Pを、辺BC上に点Qを、辺CA上に点Rを、頂点とは異なるようにとる。この3点がそれぞれの辺上を動くとき、この3点を頂点とする三角形の重心はどのような範囲を動くか図示せよ。
【考え方】
ベクトルを使って解くのがいいでしょう。
Aを基準にするなどして、文字を減らすのが普通のやり方ですが、ここでは対称性を使って考えていくほうがきれいに解けます。動くものが3つありますが、一度に全部動かすのは大変です。1つずつ動かしてみましょう。
解答編
【問題】
$\triangle \mathrm{ ABC }$に対し、辺AB上に点Pを、辺BC上に点Qを、辺CA上に点Rを、頂点とは異なるようにとる。この3点がそれぞれの辺上を動くとき、この3点を頂点とする三角形の重心はどのような範囲を動くか図示せよ。
【解答】
$\overrightarrow{ \mathrm{ AP } }=p\overrightarrow{ \mathrm{ AB } }$、$\overrightarrow{ \mathrm{ BQ } }=q\overrightarrow{ \mathrm{ BC } }$、$\overrightarrow{ \mathrm{ CR } }=r\overrightarrow{ \mathrm{ CA } }$とする$(0\lt p,q,r \lt 1)$。
原点をOとし、三角形ABC、三角形PQRの重心を、それぞれ$\mathrm{ G },\mathrm{ G }_1$とすると、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OG } } = \frac{1}{3}(\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ OC } })
\end{eqnarray}であり、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OG }_1 }
&=&
\frac{1}{3}(\overrightarrow{ \mathrm{ OP } }+\overrightarrow{ \mathrm{ OQ } }+\overrightarrow{ \mathrm{ OR } }) \\
&=&
\frac{1}{3}\left\{
p\overrightarrow{ \mathrm{ OB } } +(1-p)\overrightarrow{ \mathrm{ OA } }
+q\overrightarrow{ \mathrm{ OC } } +(1-q)\overrightarrow{ \mathrm{ OB } }
+r\overrightarrow{ \mathrm{ OA } } +(1-r)\overrightarrow{ \mathrm{ OC } }
\right\} \\[5pt]
&=&
\frac{1}{3}(\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ OC } }) \\
& & +\frac{1}{3}(
p\overrightarrow{ \mathrm{ OB } } -p\overrightarrow{ \mathrm{ OA } }
+q\overrightarrow{ \mathrm{ OC } } -q\overrightarrow{ \mathrm{ OB } }
+r\overrightarrow{ \mathrm{ OA } } -r\overrightarrow{ \mathrm{ OC } }
) \\[5pt]
&=&
\overrightarrow{ \mathrm{ OG } }
+\frac{p}{3}\overrightarrow{ \mathrm{ AB } }
+\frac{q}{3}\overrightarrow{ \mathrm{ BC } }
+\frac{r}{3}\overrightarrow{ \mathrm{ CA } }
\end{eqnarray}となる。
ここで、辺ABを三等分し、Aに近い方から$\mathrm{ A }_1$、$\mathrm{ A }_2$とおく。辺BC、辺CAも三等分し、同様に、$\mathrm{ B }_1$、$\mathrm{ B }_2$、$\mathrm{ C }_1$、$\mathrm{ C }_2$とおく。
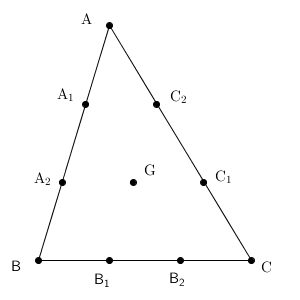

また、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OG } } +\frac{1}{3}\overrightarrow{ \mathrm{ BC } }
&=&
\frac{2}{3}\overrightarrow{ \mathrm{ OC } }+\frac{1}{3}\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OC }_1 }
\end{eqnarray}なので、$0\lt p,q \lt 1$を動くとき、$\overrightarrow{ \mathrm{ OG } } +\frac{p}{3}\overrightarrow{ \mathrm{ AB } }+\frac{q}{3}\overrightarrow{ \mathrm{ CA } }$は次の平行四辺形内を動く(境界線上の点は除く)。

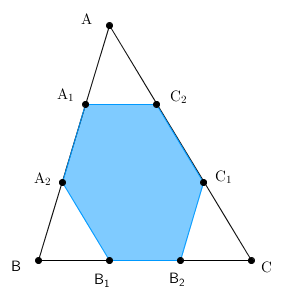
【解答終】
【解説】
三角形PQRの重心を計算すると、元の三角形ABCの重心が出てくるので、ここを基準にすると考えやすくなります。
ただ、抽象的な問題なので、なかなか解きにくいと思います。





