京都大学 文系 2019年度 第2問 解説
問題編
問題
a は実数とし、b は正の定数とする。 x の関数 $f(x)=x^2+2(ax+b|x|)$ の最小値 m を求めよ。さらに、a の値が変化するとき、 a の値を横軸に、 m の値を縦軸にとって m のグラフをかけ。
考え方
文字が多くて紛らわしいですが、 $b$ だけは変わらないことに注意しましょう。
絶対値が入っているので、場合分けをして絶対値を外して考えます。そうすると、二次関数の最小値を考えることになります。ただ、 $a$ がどのような値か、 $b$ とどのような関係かによって、頂点の位置が変わってきます。その時々で考えている区間の中に頂点の x 座標が含まれるかどうかで考えていきましょう。
最小値が求まればグラフをかくのは簡単です。
解答編
問題
a は実数とし、b は正の定数とする。 x の関数 $f(x)=x^2+2(ax+b|x|)$ の最小値 m を求めよ。さらに、a の値が変化するとき、 a の値を横軸に、 m の値を縦軸にとって m のグラフをかけ。
解答
$x\geqq 0$ のときは
\begin{eqnarray}
f(x)
&=&
x^2+2(ax+bx) \\[5pt]
&=&
(x+a+b)^2-(a+b)^2 \\[5pt]
\end{eqnarray}となる。この二次関数の頂点の x 座標は $-a-b$ であり、これが考えている区間 $x\geqq 0$ に入るのは $-a-b\geqq 0$ のとき、つまり、 $a\leqq -b$ のときである。
$x\lt 0$ のときは
\begin{eqnarray}
f(x)
&=&
x^2+2(ax-bx) \\[5pt]
&=&
(x+a-b)^2-(a-b)^2 \\[5pt]
\end{eqnarray}となる。この二次関数の頂点の x 座標は $-a+b$ であり、これが考えている区間 $x\lt 0$ に入るのは $-a+b\lt 0$ のとき、つまり、 $a\gt b$ のときである。
$b$ は正なので、以上から、 $a\leqq -b$, $-b\lt a \leqq b$, $a\gt b$ の3つの場合に分けて、 $f(x)$ の最小値を考える。
(i) $a\leqq -b$ のとき
このとき、 $-a-b\geqq 0$ なので、 $x\geqq 0$ では、 $x=-a-b$ のときに最小値 $-(a+b)^2$ をとる。この値は負である。
$b\gt 0$ より $-a+b\geqq 0$ なので、 $x\lt 0$ では、 $f(x)\gt f(0)=0$ となる。

以上から、このとき $m=-(a+b)^2$ である。
(ii) $-b\lt a \leqq b$ のとき
このとき、 $-a-b\lt 0$ なので、 $x\geqq 0$ では、 $f(x)$ は $x=0$ で最小値 $f(0)=0$ をとる。
また、 $-a+b\geqq 0$ なので、 $x\lt 0$ では、 $f(x)\gt f(0)=0$ となる。
以上から、このとき $m=0$ である。
(iii) $a\gt b$ のとき
このとき、 $-a-b\lt 0$ なので、 $x\geqq 0$ では、 $x=0$ のときに最小値 $f(0)=0$ をとる。
また、 $-a+b\lt 0$ なので、 $x\lt 0$ では、 $x=-a+b$ のときに最小値 $-(a-b)^2$ をとる。この値は負である。

以上から、このとき $m=-(a-b)^2$ である。
(i)(ii)(iii) より、
\begin{eqnarray}
m
=
\begin{cases}
-(a+b)^2 & ( a \leqq -b ) \\
0 & ( -b \lt a \leqq b ) \\
-(a-b)^2 & ( a \gt b )
\end{cases}
\end{eqnarray}
となる。 $b\gt 0$ より、 m のグラフは次のようになる。
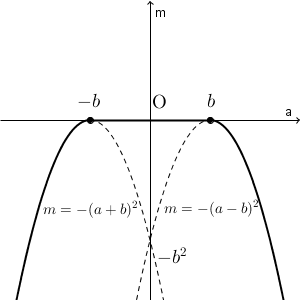
(終)





