センター試験 数学II・数学B 2020年度追試 第4問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
1辺の長さが $1$ のひし形 ABCD において、 $\angle \mathrm{BAD} \gt 90^{\circ}$ とする。直線 BC 上に、点 C とは異なる点 E を、 $|\overrightarrow{ \mathrm{ DE } }|=1$ を満たすようにとる。以下、 $\overrightarrow{ \mathrm{ AB } }=\vec{p}$, $\overrightarrow{ \mathrm{ AD } }=\vec{q}$ とし、 $\vec{p}\cdot \vec{q}=x$ とおく。
(1) $|\overrightarrow{ \mathrm{ BD } }|^2=\myBox{ア}-\myBox{イ}x$ である。
(2) $\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ BE } }$ は平行なので、実数 $s$ を用いて $\overrightarrow{ \mathrm{ AE } }=\vec{p}+s\vec{q}$ と表すことができる。 $|\overrightarrow{ \mathrm{ DE } }|=1$ であることと、点 E は点 C と異なる点であることにより、 $s=\myBox{ウエ}x+\myBox{オ}$ である。
(3) $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ を満たす $x$ の値を求めよう。
(2)により、 $\overrightarrow{ \mathrm{ AE } }=\vec{p}+\left(\mybox{ウエ}x+\mybox{オ}\right)\vec{q}$ である。 $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ と $\angle \mathrm{BAD}\gt 90^{\circ}$ により、 $x=\dfrac{\myBox{カ}-\sqrt{\myBox{キ} }}{\myBox{ク} }$ が得られる。
したがって\[ \overrightarrow{ \mathrm{ AE } }=\vec{p}+\frac{\myBox{ケ}+\sqrt{\myBox{コ} }}{\myBox{サ} } \vec{q} \quad\cdots ① \]である。
(4) $x$ を(3)で求めた値とし、点 F を直線 AC に関して点 E と対称な点とする。 $|\overrightarrow{ \mathrm{ EF } }|$ を求めよう。
点 B と点 D が直線 AC に関して対称な点であることに注意すると、①により、 $\overrightarrow{ \mathrm{ AF } }=\dfrac{\myBox{シ}+\sqrt{\myBox{ス} }}{\myBox{セ} }\vec{p}+\vec{q}$ と表せる。したがって、 $\overrightarrow{ \mathrm{ EF } }=\dfrac{\myBox{ソタ}+\sqrt{\myBox{チ} }}{\myBox{ツ} }\overrightarrow{ \mathrm{ DB } }$ である。
また、 $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ であり、(2)により $\overrightarrow{ \mathrm{ BE } }=\left(\mybox{ウエ}x+\mybox{オ}\right)\vec{q}$ となるので、 $|\overrightarrow{ \mathrm{ BD } }|=\dfrac{\myBox{テ}+\sqrt{\myBox{ト} }}{\myBox{ナ} }$ を得る。ゆえに、 $|\overrightarrow{ \mathrm{ EF } }|=\myBox{ニ}$ である。
(5) $x$ を(3)で求めた値とし、点 R を $\triangle \mathrm{ ABD }$ の外接円の中心とする。 $\overrightarrow{ \mathrm{ AR } }$ を $\vec{p}$ と $\vec{q}$ を用いて表そう。
$\triangle \mathrm{ ABD }$ は $\mathrm{AB}=\mathrm{AD}$ を満たす二等辺三角形であるから、点 R は直線 AC 上にある。点 F を(4)で定めた点とし、線分 AD の中点を M とする。(4)の結果を用いることにより、 $\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ FM } }$ は垂直であることが確かめられる。よって、点 R は直線 AC と直線 FM の交点であり、実数 $t$ を用いて $\overrightarrow{ \mathrm{ AR } }=t \overrightarrow{ \mathrm{ AF } }+(1-t)\overrightarrow{ \mathrm{ AM } }$ と表すことができる。 $t$ を求めることにより、 $\overrightarrow{ \mathrm{ AR } }=\dfrac{\myBox{ヌ}+\sqrt{\myBox{ネ} }}{\myBox{ノハ} } \left(\vec{p}+\vec{q}\right)$ が得られる。
考え方
計算は少し大変ですが、誘導は丁寧なので、進めていくこと自体はできると思います。ただ、どんな図形を扱っているのかは、きれいな図をかかないと気づきにくいかもしれません(気づいたところで計算が楽になるわけではないですが)。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
1辺の長さが $1$ のひし形 ABCD において、 $\angle \mathrm{BAD} \gt 90^{\circ}$ とする。直線 BC 上に、点 C とは異なる点 E を、 $|\overrightarrow{ \mathrm{ DE } }|=1$ を満たすようにとる。以下、 $\overrightarrow{ \mathrm{ AB } }=\vec{p}$, $\overrightarrow{ \mathrm{ AD } }=\vec{q}$ とし、 $\vec{p}\cdot \vec{q}=x$ とおく。
(1) $|\overrightarrow{ \mathrm{ BD } }|^2=\myBox{ア}-\myBox{イ}x$ である。
解説
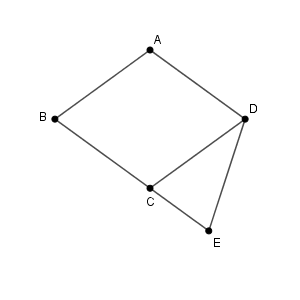
四角形 ABCD は1辺の長さが $1$ のひし形なので、 $\overrightarrow{ \mathrm{ AB } }$ も $\overrightarrow{ \mathrm{ AD } }$ も大きさは $1$ です。なので、
\begin{eqnarray}
|\overrightarrow{ \mathrm{ BD } }|^2
&=&
|\overrightarrow{ \mathrm{ AD } }-\overrightarrow{ \mathrm{ AB } }|^2 \\[5pt]
&=&
|\overrightarrow{ \mathrm{ AD } }|^2 -2\overrightarrow{ \mathrm{ AD } }\cdot \overrightarrow{ \mathrm{ AD } }+|\overrightarrow{ \mathrm{ AB } }|^2 \\[5pt]
&=&
1 -2x+1 \\[5pt]
&=&
2-2x
\end{eqnarray}となります。
解答
アイ:22
解答編 つづき
問題
(2) $\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ BE } }$ は平行なので、実数 $s$ を用いて $\overrightarrow{ \mathrm{ AE } }=\vec{p}+s\vec{q}$ と表すことができる。 $|\overrightarrow{ \mathrm{ DE } }|=1$ であることと、点 E は点 C と異なる点であることにより、 $s=\myBox{ウエ}x+\myBox{オ}$ である。
解説

$\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ BE } }$ は平行なので、 $\overrightarrow{ \mathrm{ BE } }=s\overrightarrow{ \mathrm{ AD } }=s\vec{q}$ となる実数 $s$ が存在します。これより、 $\overrightarrow{ \mathrm{ AE } }=\vec{p}+s\vec{q}$ と書ける、というのが問題文の前半で書いてあることです。
$|\overrightarrow{ \mathrm{ DE } }|=1$ となるように点 E をとっているので、これをもとに $s$ を求めます。
\begin{eqnarray}
|\overrightarrow{ \mathrm{ DE } }|^2 &=& 1 \\[5pt]
|\overrightarrow{ \mathrm{ AE } }-\overrightarrow{ \mathrm{ AD } }|^2 &=& 1 \\[5pt]
|\vec{p}+s\vec{q}-\vec{q}|^2 &=& 1 \\[5pt]
|\vec{p}|^2+2(s-1)\vec{p}\cdot\vec{q}+(s-1)^2|\vec{q}|^2 &=& 1 \\[5pt]
1+2(s-1)x+(s-1)^2\cdot 1 &=& 1 \\[5pt]
1+2sx-2x+s^2-2s+1 &=& 1 \\[5pt]
s^2+(2x-2)s-2x+1 &=& 0 \\[5pt]
(s-1)(s+2x-1) &=& 0 \\[5pt]
s &=& 1,-2x+1
\end{eqnarray}となります。後半の因数分解は少し難しいかもしれません。しかし、 $|\overrightarrow{ \mathrm{ DC } }|=1$ であり、 $\vec{p}+1\cdot\vec{q}=\overrightarrow{ \mathrm{ AC } }$ と書けることから、 $s=1$ という解を持つことがわかるので、これに気づけば計算しやすくなります。これに気づかなければ、頑張って因数分解を思いつくか、最悪、二次方程式の解の公式で解くことになります。
$s=1$ は今の状況には適さない(点 E が点 C と一致してしまうため)ので、 $s=-2x+1$ となります。
解答
ウエオ:-21
解答編 つづき
問題
(3) $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ を満たす $x$ の値を求めよう。
(2)により、 $\overrightarrow{ \mathrm{ AE } }=\vec{p}+\left(\mybox{ウエ}x+\mybox{オ}\right)\vec{q}$ である。 $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ と $\angle \mathrm{BAD}\gt 90^{\circ}$ により、 $x=\dfrac{\myBox{カ}-\sqrt{\myBox{キ} }}{\myBox{ク} }$ が得られる。
したがって\[ \overrightarrow{ \mathrm{ AE } }=\vec{p}+\frac{\myBox{ケ}+\sqrt{\myBox{コ} }}{\myBox{サ} } \vec{q} \quad\cdots ① \]である。
解説
\begin{eqnarray} & & |\overrightarrow{ \mathrm{ BE } }| \\[5pt] &=& |\overrightarrow{ \mathrm{ AE } }-\overrightarrow{ \mathrm{ AB } }| \\[5pt] &=& |\vec{p}+(-2x+1)\vec{q}-\vec{p}| \\[5pt] &=& |-2x+1| \\[5pt] \end{eqnarray}となります。これが $|\mathrm{ BD }|$ と等しくなる $x$ を求めます。 \begin{eqnarray} |\mathrm{ BD }|^2 &=& |\mathrm{ BE }|^2 \\[5pt] 2-2x &=& (-2x+1)^2 \\[5pt] 2-2x &=& 4x^2-4x+1 \\[5pt] 4x^2-2x-1 &=& 0 \\[5pt] x &=& \frac{2\pm\sqrt{4+16} }{8} \\[5pt] &=& \frac{1\pm\sqrt{5} }{4} \\[5pt] \end{eqnarray}となります。ここで、 $x=\vec{p}\cdot\vec{q}=\cos\angle \mathrm{ BAD }$ であり、 $\angle \mathrm{ BAD }$ は鈍角だから $x\lt 0$ です。なので、\[ x=\dfrac{1-\sqrt{5} }{4} \]となります。これより
\begin{eqnarray}
\overrightarrow{ \mathrm{ AE } }
&=&
\vec{p} +(-2x+1)\vec{q} \\[5pt]
&=&
\vec{p} +\left(-2\cdot\frac{1-\sqrt{5} }{4}+1\right)\vec{q} \\[5pt]
&=&
\vec{p} +\left(\frac{-1+\sqrt{5} }{2}+1\right)\vec{q} \\[5pt]
&=&
\vec{p} +\frac{1+\sqrt{5} }{2}\vec{q} \\[5pt]
\end{eqnarray}となります。
解答
カキク:154
ケコサ:152
解答編 つづき
問題
(4) $x$ を(3)で求めた値とし、点 F を直線 AC に関して点 E と対称な点とする。 $|\overrightarrow{ \mathrm{ EF } }|$ を求めよう。
点 B と点 D が直線 AC に関して対称な点であることに注意すると、①により、 $\overrightarrow{ \mathrm{ AF } }=\dfrac{\myBox{シ}+\sqrt{\myBox{ス} }}{\myBox{セ} }\vec{p}+\vec{q}$ と表せる。したがって、 $\overrightarrow{ \mathrm{ EF } }=\dfrac{\myBox{ソタ}+\sqrt{\myBox{チ} }}{\myBox{ツ} }\overrightarrow{ \mathrm{ DB } }$ である。
また、 $|\overrightarrow{ \mathrm{ BD } }|=|\overrightarrow{ \mathrm{ BE } }|$ であり、(2)により $\overrightarrow{ \mathrm{ BE } }=\left(\mybox{ウエ}x+\mybox{オ}\right)\vec{q}$ となるので、 $|\overrightarrow{ \mathrm{ BD } }|=\dfrac{\myBox{テ}+\sqrt{\myBox{ト} }}{\myBox{ナ} }$ を得る。ゆえに、 $|\overrightarrow{ \mathrm{ EF } }|=\myBox{ニ}$ である。
解説
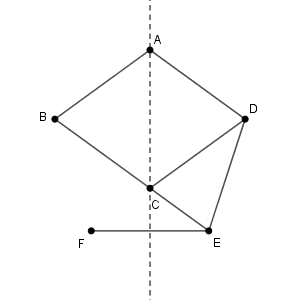
点 B と点 D が直線 AC について対称であり、 点 E と点 F が直線 AC について対称であることから、対称性より、 $\overrightarrow{ \mathrm{ AE } }$ を $\overrightarrow{ \mathrm{ AB } }, \overrightarrow{ \mathrm{ AD } }$ で表した式で、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ AD } }$ を入れ替えると $\overrightarrow{ \mathrm{ AF } }$ を表す式になります。つまり、(3)の結果から\[ \overrightarrow{ \mathrm{ AF } }=\frac{1+\sqrt{5} }{2}\vec{p}+\vec{q} \]ということです。
これより
\begin{eqnarray}
\overrightarrow{ \mathrm{ EF } }
&=&
\overrightarrow{ \mathrm{ AF } }-\overrightarrow{ \mathrm{ AE } } \\[5pt]
&=&
\left(\frac{1+\sqrt{5} }{2}\vec{p}+\vec{q}\right)-\left(\vec{p} +\frac{1+\sqrt{5} }{2}\vec{q}\right) \\[5pt]
&=&
\frac{-1+\sqrt{5} }{2} \left(\vec{p}-\vec{q}\right) \\[5pt]
&=&
\frac{-1+\sqrt{5} }{2} \overrightarrow{ \mathrm{ DB } } \\[5pt]
\end{eqnarray}となります。
また、問題文にそって $|\overrightarrow{ \mathrm{ BD } }|$ を求めると
\begin{eqnarray}
|\overrightarrow{ \mathrm{ BD } }|
&=&
|\overrightarrow{ \mathrm{ BE } }| \\[5pt]
&=&
|(-2x+1)\vec{q}| \\[5pt]
&=&
|-2x+1| \\[5pt]
&=&
\left|-2\cdot \frac{1-\sqrt{5} }{4}+1\right| \\[5pt]
&=&
\left|\frac{-1+\sqrt{5} }{2}+1\right| \\[5pt]
&=&
\frac{1+\sqrt{5} }{2} \\[5pt]
\end{eqnarray}となります。このことから
\begin{eqnarray}
|\overrightarrow{ \mathrm{ EF } }|
&=&
\left| \frac{-1+\sqrt{5} }{2} \overrightarrow{ \mathrm{ DB } } \right| \\[5pt]
&=&
\frac{-1+\sqrt{5} }{2} \left|\overrightarrow{ \mathrm{ DB } } \right| \\[5pt]
&=&
\frac{-1+\sqrt{5} }{2} \cdot \frac{1+\sqrt{5} }{2} \\[5pt]
&=&
\frac{5-1}{4}=1
\end{eqnarray}となります。
解答
シスセ:152
ソタチツ:-152
テトナ:152
ニ:1
解答編 つづき
問題
(5) $x$ を(3)で求めた値とし、点 R を $\triangle \mathrm{ ABD }$ の外接円の中心とする。 $\overrightarrow{ \mathrm{ AR } }$ を $\vec{p}$ と $\vec{q}$ を用いて表そう。
$\triangle \mathrm{ ABD }$ は $\mathrm{AB}=\mathrm{AD}$ を満たす二等辺三角形であるから、点 R は直線 AC 上にある。点 F を(4)で定めた点とし、線分 AD の中点を M とする。(4)の結果を用いることにより、 $\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ FM } }$ は垂直であることが確かめられる。よって、点 R は直線 AC と直線 FM の交点であり、実数 $t$ を用いて $\overrightarrow{ \mathrm{ AR } }=t \overrightarrow{ \mathrm{ AF } }+(1-t)\overrightarrow{ \mathrm{ AM } }$ と表すことができる。 $t$ を求めることにより、 $\overrightarrow{ \mathrm{ AR } }=\dfrac{\myBox{ヌ}+\sqrt{\myBox{ネ} }}{\myBox{ノハ} } \left(\vec{p}+\vec{q}\right)$ が得られる。
解説
誘導に沿って解いていきます。
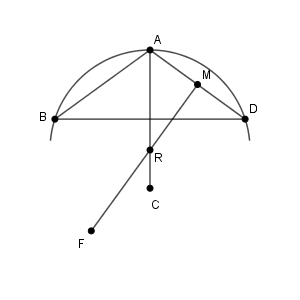
一応、問題文に書いてあることを確かめます。AD の中点を M としているので、 $\overrightarrow{ \mathrm{ AM } }=\dfrac{\vec{q} }{2}$ です。なので、
\begin{eqnarray}
\overrightarrow{ \mathrm{ FM } }
&=&
\overrightarrow{ \mathrm{ AM } }-\overrightarrow{ \mathrm{ AF } } \\[5pt]
&=&
\frac{\vec{q} }{2}-\left(\frac{1+\sqrt{5} }{2}\vec{p}+\vec{q}\right) \\[5pt]
&=&
-\frac{1+\sqrt{5} }{2}\vec{p}-\frac{\vec{q} }{2} \\[5pt]
\end{eqnarray}となることから、
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ AD } }\cdot \overrightarrow{ \mathrm{ FM } } \\[5pt]
&=&
\vec{q}\cdot \left(-\frac{1+\sqrt{5} }{2}\vec{p}-\frac{\vec{q} }{2}\right) \\[5pt]
&=&
-\frac{1+\sqrt{5} }{2}x-\frac{|\vec{q}|^2}{2} \\[5pt]
&=&
-\frac{1+\sqrt{5} }{2}\cdot\frac{1-\sqrt{5} }{4}-\frac{1}{2} \\[5pt]
&=&
-\frac{1-5}{8}-\frac{1}{2} \\[5pt]
&=&
0
\end{eqnarray}となるので、たしかに、 $\overrightarrow{ \mathrm{ AD } }$ と $\overrightarrow{ \mathrm{ FM } }$ は垂直であることがわかります。
外接円の中心は、各辺の垂直二等分線上にあるので、点 R は直線 AC と直線 FM の交点です。ここで、 $\mathrm{ FR }:\mathrm{ RM }=(1-t):t$ と置けば、\[ \overrightarrow{ \mathrm{ AR } }=t\overrightarrow{ \mathrm{ AF } }+(1-t)\overrightarrow{ \mathrm{ AM } } \]と書けます。これを変形すると
\begin{eqnarray}
\overrightarrow{ \mathrm{ AR } }
&=&
t\overrightarrow{ \mathrm{ AF } }+(1-t)\overrightarrow{ \mathrm{ AM } } \\[5pt]
&=&
t\left(\frac{1+\sqrt{5} }{2}\vec{p}+\vec{q}\right)+(1-t)\frac{1}{2}\vec{q} \\[5pt]
&=&
\frac{t(1+\sqrt{5})}{2}\vec{p}+\frac{1+t}{2}\vec{q} \\[5pt]
\end{eqnarray}となります。ここで、点 R は直線 AC 上の点でもあり、 $\overrightarrow{ \mathrm{ AC } }=\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ AD } }=\vec{p}+\vec{q}$ なので、 $\overrightarrow{ \mathrm{ AR } }$ の $\vec{p}$ と $\vec{q}$ の係数は等しくなります。よって、
\begin{eqnarray}
\frac{t(1+\sqrt{5})}{2} &=& \frac{1+t}{2} \\[5pt]
t+t\sqrt{5} &=& 1+t \\[5pt]
t &=& \frac{\sqrt{5} }{5} \\[5pt]
\end{eqnarray}となります。これを代入して
\begin{eqnarray}
\overrightarrow{ \mathrm{ AR } }
&=&
\frac{t(1+\sqrt{5})}{2}\vec{p}+\frac{1+t}{2}\vec{q} \\[5pt]
&=&
\frac{\sqrt{5}+5}{10}\vec{p}+\frac{5+\sqrt{5} }{10}\vec{q} \\[5pt]
&=&
\frac{5+\sqrt{5} }{10}\left(\vec{p}+\vec{q}\right) \\[5pt]
\end{eqnarray}となります。
ちなみに、この図形をよく考えてみましょう。 $\mathrm{ AB }=\mathrm{ AD }=1$ で、 $\mathrm{ DE }=1$, $\mathrm{ BD }=\mathrm{ BE }$ となるように点 $\mathrm{ E }$ をとりました。また、対称性から、 $\mathrm{ BF }=1$, $\mathrm{ DB }=\mathrm{ DF }$ も成り立ちます。さらに、(4)で求めたように、 $\mathrm{ EF }=1$ です。
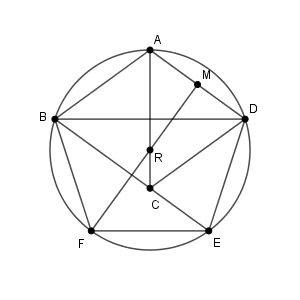
この問題の(3)以降は、実は、正五角形 ABFED をかいていたことになります。
解答
ヌネノハ:5510





