センター試験 数学II・数学B 2020年度追試 第1問 [1] 解説
【必答問題】
問題編
問題
関数 $y=-2^{2x}+2^{x+4}-48$ について考える。
(1) $t=2^x$ とおく。 $y$ を $t$ の式で表すと\[ y=\myBox{ア}\left(t-\myBox{イ}\right)^2+\myBox{ウエ} \]となる。
$x=1$ のとき、 $y=\myBox{オカキ}$ である。 $x\geqq 1$ のとき、 $y$ は $x=\myBox{ク}$ で最大値 $\myBox{ケコ}$ をとる。
(2) $k\gt 1$ とする。 $x$ が $1\leqq x\leqq k$ の範囲を動くとき、 $y$ の最小値が $\mybox{オカキ}$ であるような $k$ の値の範囲は\[ 1\lt k\leqq \log_2\myBox{サシ} \]である。この範囲に含まれる最大の整数の値は $\myBox{ス}$ である。
(3) $y=0$ を満たす $x$ は二つある。そのうちの小さい方は $\myBox{セ}$ である。また、大きい方は $\myBox{ソ}$ を満たす。 $\myBox{ソ}$ に当てはまるものを、次の 0 ~ 9 のうちから一つ選べ。ただし、 $\log_{10}2=0.3010$, $\log_{10}3=0.4771$ とする。
0: $1\lt x\lt 1.2$
1: $1.2\lt x\lt 1.3$
2: $1.5\lt x\lt 1.6$
3: $2.4\lt x\lt 2.5$
4: $2.5\lt x\lt 2.6$
5: $2.6\lt x\lt 2.8$
6: $3.5\lt x\lt 3.6$
7: $3.6\lt x\lt 3.8$
8: $4.2\lt x\lt 4.4$
9: $x\gt 10$
考え方
変換して関数の最大値や最小値を考えるのは、よくある問題です。最後は、与えられた常用対数の値が使えるようにうまく変形します。
【必答問題】
解答編
問題
関数 $y=-2^{2x}+2^{x+4}-48$ について考える。
(1) $t=2^x$ とおく。 $y$ を $t$ の式で表すと\[ y=\myBox{ア}\left(t-\myBox{イ}\right)^2+\myBox{ウエ} \]となる。
解説
\begin{eqnarray} y &=& -2^{2x}+2^{x+4}-48 \\[5pt] &=& -\left(2^{x}\right)^2 +16\cdot 2^x-48 \\[5pt] &=& -t^2 +16t-48 \\[5pt] &=& -(t-8)^2+64-48 \\[5pt] &=& -(t-8)^2+16 \\[5pt] \end{eqnarray}となります。解答
アイウエ:-816
解答編 つづき
問題
$x=1$ のとき、 $y=\myBox{オカキ}$ である。 $x\geqq 1$ のとき、 $y$ は $x=\myBox{ク}$ で最大値 $\myBox{ケコ}$ をとる。
解説
$x=1$ のとき $t=2$ なので
\begin{eqnarray}
y=-(2-8)^2+16=-20
\end{eqnarray}となります。
また、 $x\geqq 1$ のとき $t\geqq 2$ なので、 $y=-(t-8)^2+16$ は $t=8$ のときに最大値 $16$ をとります。

$2^x=8$ のとき $x=3$ なので、 $y$ は $x=3$ のときに最大値 $16$ をとることがわかります。
解答
オカキ:-20
ク:3
ケコ:16
解答編 つづき
問題
(2) $k\gt 1$ とする。 $x$ が $1\leqq x\leqq k$ の範囲を動くとき、 $y$ の最小値が $\mybox{オカキ}$ であるような $k$ の値の範囲は\[ 1\lt k\leqq \log_2\myBox{サシ} \]である。この範囲に含まれる最大の整数の値は $\myBox{ス}$ である。
解説
$1\leqq x\leqq k$ のとき、 $2\leqq t\leqq 2^k$ です。このとき、 $y=-(t-8)^2+16$ のグラフは次のようになります。
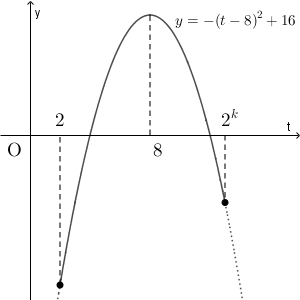
$y$ の最小値が $-20$ となることは、区間の端と放物線の軸との距離を考えると、 $8-2\geqq 2^k-8$ と同値です。このことから、 $k$ の範囲は\[ 1\lt k \leqq \log_2 14 \]となります。 $2^3=8$, $2^4=16$ なので、これを満たす最大の整数は $3$ です。
解答
サシ:14
ス:3
解答編 つづき
問題
(3) $y=0$ を満たす $x$ は二つある。そのうちの小さい方は $\myBox{セ}$ である。また、大きい方は $\myBox{ソ}$ を満たす。 $\myBox{ソ}$ に当てはまるものを、次の 0 ~ 9 のうちから一つ選べ。ただし、 $\log_{10}2=0.3010$, $\log_{10}3=0.4771$ とする。
0: $1\lt x\lt 1.2$
1: $1.2\lt x\lt 1.3$
2: $1.5\lt x\lt 1.6$
3: $2.4\lt x\lt 2.5$
4: $2.5\lt x\lt 2.6$
5: $2.6\lt x\lt 2.8$
6: $3.5\lt x\lt 3.6$
7: $3.6\lt x\lt 3.8$
8: $4.2\lt x\lt 4.4$
9: $x\gt 10$
解説
\begin{eqnarray} y &=& -t^2 +16t-48 \\[5pt] &=& -(t^2-16t+48) \\[5pt] &=& -(t-4)(t-12) \\[5pt] \end{eqnarray}となります。なので、小さい方の解は $t=4$ のときなので、このときの $x$ は $\log_2 4=2$ です。大きい方の解は $\log_2 12$ です。これを変形すると
\begin{eqnarray}
\log_2 12
&=&
\log_2 2^2\cdot 3 \\[5pt]
&=&
2+\log_2 3 \\[5pt]
&=&
2+\frac{\log_{10} 3}{\log_{10} 2} \\[5pt]
&=&
2+\frac{0.4771}{0.3010} \\[5pt]
&=&
3.58\cdots
\end{eqnarray}となります(途中で、底の変換公式を使っています)。選択肢の中では 6 が正しいことがわかります。
解答
セ:2
ソ:6





