センター試験 数学I・数学A 2014年度追試 第3問 解説
【必答問題】
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$$\triangle \mathrm{ ABC }$ を $\mathrm{ AB }=8$, $\mathrm{ BC }=12$, $\mathrm{ CA }=10$ を満たす三角形とする。辺 AB の中点を D 、辺 BC の中点を E とする。このとき、 $\displaystyle \sin \angle \mathrm{ DBE } =\frac{\myBox{ア}\sqrt{\myBox{イ} }}{\myBox{ウエ} }$ 、 $\triangle \mathrm{ DBE }$ の面積は $\displaystyle \frac{\myBox{オカ}\sqrt{\myBox{キ} }}{\myBox{ク} }$ である。 $\triangle \mathrm{ DBE }$ の内心を I とする。
(1) 内接円 I の半径は $\displaystyle \frac{\sqrt{\myBox{ケ} }}{\myBox{コ} }$ である。円 I と辺 BE の接点を L とすると、 $\displaystyle \mathrm{ BL }=\frac{\myBox{サ} }{\myBox{シ} }$ であるので、 $\mathrm{ BI }=\myBox{ス}\sqrt{\myBox{セ} }$ である。
三つの線分 AD, CE, DE すべてに接する円の中心を J とする。円 J と線分 CE との接点を X 、 線分 DE との接点を Y 、線分 AD との接点を Z とする。
(2) 直線 BX, BZ はともに点 B から円 J に引いた接線であるので、 $\mathrm{ BX }=\mathrm{ BZ }$ である。これより $\displaystyle \mathrm{ EX }=\frac{\myBox{ソ} }{\myBox{タ} }$ である。 $\displaystyle \angle \mathrm{ JBE }=\frac{\myBox{チ} }{\myBox{ツ} }\angle \mathrm{ DBE }$ 、 $\displaystyle \angle \mathrm{ IBE }=\frac{\myBox{テ} }{\myBox{ト} }\angle \mathrm{ DBE }$ より $\mathrm{ BJ } = \myBox{ナ} \sqrt{\myBox{ニ} }$ である。
(3) $\angle \mathrm{ DBE }$ を含む平面と垂直で、直線 BJ を含む平面を考え、この平面内にある円で、線分 BJ を直径とするものを O とする。この円 O の円周上に点 K を、 BJ と KI が直交するようにとると、 $\mathrm{ KI }=\myBox{ヌ}$ となるので、三角錐 KBDE の体積は $\myBox{ネ}\sqrt{\myBox{ノ} }$ となる。
考え方
(1)より前の部分は、まず $\cos$ から考えましょう。(1)は三角形の面積とからめて半径を求めます。また、 BL は長さを2通りに表して方程式を作りましょう。
(2)は少し図が描きづらいです。 EX はさきほどの BL を求めたときと同様に、長さを2通りに表して方程式を作ります。
(3)は突然三次元の話になりますが、そんなに複雑ではありません。円 O を含む平面で切って考えれば、 KI を求めることはそれほど難しくありません。これが高さとなり、底面積はすでに求めてあるので、体積もすぐに出せます。
三角比に関する問題は(1)までで、その後はほぼ図形の問題です。
【必答問題】
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$$\triangle \mathrm{ ABC }$ を $\mathrm{ AB }=8$, $\mathrm{ BC }=12$, $\mathrm{ CA }=10$ を満たす三角形とする。辺 AB の中点を D 、辺 BC の中点を E とする。このとき、 $\displaystyle \sin \angle \mathrm{ DBE } =\frac{\myBox{ア}\sqrt{\myBox{イ} }}{\myBox{ウエ} }$ 、 $\triangle \mathrm{ DBE }$ の面積は $\displaystyle \frac{\myBox{オカ}\sqrt{\myBox{キ} }}{\myBox{ク} }$ である。
解説
図は次のようになっています。
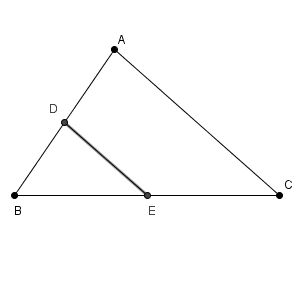
$\sin$ をいきなり求めるのは無理なので、まずは $\cos$ から求めます。
$\mathrm{ DB }=4$, $\mathrm{ BE }=6$ であり、中点連結定理から $\mathrm{ DE }=5$ となります。よって、余弦定理から
\begin{eqnarray}
\cos \angle \mathrm{ DBE }
&=&
\frac{4^2+6^2-5^2}{2\cdot 4\cdot 6} \\[5pt]
&=&
\frac{27}{2\cdot 4\cdot 6} \\[5pt]
&=&
\frac{9}{16} \\[5pt]
\end{eqnarray}となります。
三角比の相互関係から
\begin{eqnarray}
\sin \angle \mathrm{ DBE }
&=&
\sqrt{1-\left(\frac{9}{16}\right)^2} \\[5pt]
&=&
\frac{\sqrt{256-81} }{16} \\[5pt]
&=&
\frac{\sqrt{175} }{16} \\[5pt]
&=&
\frac{5\sqrt{7} }{16} \\[5pt]
\end{eqnarray}が得られます。
また、三角形 DBE の面積は
\begin{eqnarray}
& &
\frac{1}{2}\times \mathrm{ DB }\cdot \mathrm{ BE } \sin \angle \mathrm{ DBE } \\[5pt]
&=&
\frac{1}{2}\times 4\cdot 6\cdot \frac{5\sqrt{7} }{16} \\[5pt]
&=&
\frac{15\sqrt{7} }{4} \\[5pt]
\end{eqnarray}となります。
解答
アイウエ:5716
オカキク:1574
参考
解答編 つづき
問題
$\triangle \mathrm{ DBE }$ の内心を I とする。
(1) 内接円 I の半径は $\displaystyle \frac{\sqrt{\myBox{ケ} }}{\myBox{コ} }$ である。円 I と辺 BE の接点を L とすると、 $\displaystyle \mathrm{ BL }=\frac{\myBox{サ} }{\myBox{シ} }$ であるので、 $\mathrm{ BI }=\myBox{ス}\sqrt{\myBox{セ} }$ である。
解説
図は次のようになっています。
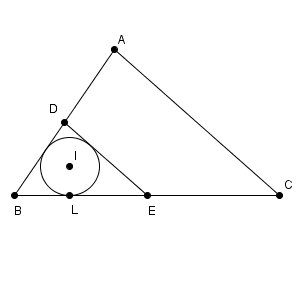
内接円 I の半径を r とすると、三角形 DBE の面積は次のように書くこともできます。
\begin{eqnarray}
\frac{r}{2}(\mathrm{ DB }+\mathrm{ BE }+\mathrm{ ED })
\end{eqnarray}よって、先ほどの結果から、次のようにして r を求めることができます。
\begin{eqnarray}
\frac{r}{2}(4+6+5) &=& \frac{15\sqrt{7} }{4} \\[5pt]
r &=& \frac{\sqrt{7} }{2} \\[5pt]
\end{eqnarray}

$\mathrm{ BL }=x$ とします。 B から円 I に接線を引いたと考えれば、 DB 上の接点と B との距離は x であり、 DB 上の接点と D との距離は $4-x$ となります。同様に考えると、\[ \mathrm{ EL } = 5-(4-x)=x+1 \]となります。また、 $\mathrm{ EL }=6-x$ も成り立つので、
\begin{eqnarray}
x+1 &=& 6-x \\[5pt]
2x &=& 5 \\[5pt]
x &=& \frac{5}{2} \\[5pt]
\end{eqnarray}となります。よって、 $\displaystyle \mathrm{ BL }=\frac{5}{2}$ です。

IL と BL は垂直に交わるので、三平方の定理から
\begin{eqnarray}
\mathrm{ BI }
&=&
\sqrt{\mathrm{ IL }^2+\mathrm{ BL }^2} \\[5pt]
&=&
\sqrt{ \left(\frac{\sqrt{7} }{2}\right) ^2+ \left(\frac{5}{2}\right)^2} \\[5pt]
&=&
\sqrt{ \frac{7}{4}+\frac{25}{4} } \\[5pt]
&=&
\sqrt{ 8 } \\[5pt]
&=&
2\sqrt{ 2 } \\[5pt]
\end{eqnarray}となります。
解答
ケコ:72サシ:52
スセ:22
参考
解答編 つづき
問題
三つの線分 AD, CE, DE すべてに接する円の中心を J とする。円 J と線分 CE との接点を X 、 線分 DE との接点を Y 、線分 AD との接点を Z とする。
(2) 直線 BX, BZ はともに点 B から円 J に引いた接線であるので、 $\mathrm{ BX }=\mathrm{ BZ }$ である。これより $\displaystyle \mathrm{ EX }=\frac{\myBox{ソ} }{\myBox{タ} }$ である。
解説
図は次のようになっています。
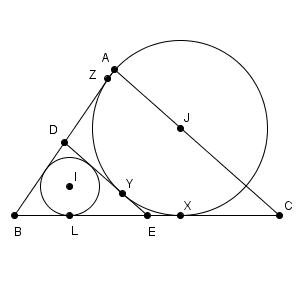
BX と BZ は、 B から円 J に引いた接線なので、 $\mathrm{ BX }=\mathrm{ BZ }$ となります。また、同様に接線に注目すると、 $\mathrm{ EX }=\mathrm{ EY }$ と $\mathrm{ DY }=\mathrm{ DZ }$ も得られます。
$\mathrm{ EX }=x$ とすると、 $\mathrm{ EY }=x$, $\mathrm{ DZ } = \mathrm{ DY }=5-x$ なので、 $\mathrm{ BZ }=4+(5-x)=9-x$ となります。また、 $\mathrm{ BX }=6+x$ なので
\begin{eqnarray}
6+x &=& 9-x \\
2x &=& 3 \\
x &=& \frac{3}{2} \\
\end{eqnarray}となります。
解答
ソタ:32
解答編 つづき
問題
$\displaystyle \angle \mathrm{ JBE }=\frac{\myBox{チ} }{\myBox{ツ} }\angle \mathrm{ DBE }$ 、 $\displaystyle \angle \mathrm{ IBE }=\frac{\myBox{テ} }{\myBox{ト} }\angle \mathrm{ DBE }$ より $\mathrm{ BJ } = \myBox{ナ} \sqrt{\myBox{ニ} }$ である。
解説

BX と BZ は、 B から円 J に引いた接線であり、円 I に引いた接線でもあるので、 $\displaystyle \angle \mathrm{ JBE }=\frac{1}{2}\angle \mathrm{ DBE }$ と $\displaystyle \angle \mathrm{ IBE }=\frac{1}{2}\angle \mathrm{ DBE }$ が成り立ちます。
よって、 B, I, J は一直線上に並んでおり、 IL と JX は平行だから、三角形 BIL と三角形 BJX は相似であることがわかるので
\begin{eqnarray}
\mathrm{ BJ }:\mathrm{ BI } &=& \mathrm{ BX }:\mathrm{ BL } \\[5pt]
\mathrm{ BJ }:2\sqrt{ 2 } &=& \left(6+\frac{3}{2}\right):\frac{5}{2} \\
&=& 3:1 \\
\mathrm{ BJ } &=& 6\sqrt{2}
\end{eqnarray}と求められます。
解答
チツ:12
テト:12
ナニ:62
解答編 つづき
問題
(3) $\angle \mathrm{ DBE }$ を含む平面と垂直で、直線 BJ を含む平面を考え、この平面内にある円で、線分 BJ を直径とするものを O とする。この円 O の円周上に点 K を、 BJ と KI が直交するようにとると、 $\mathrm{ KI }=\myBox{ヌ}$ となるので、三角錐 KBDE の体積は $\myBox{ネ}\sqrt{\myBox{ノ} }$ となる。
解説

円 O を含む平面での断面を考えると、次のようになります。
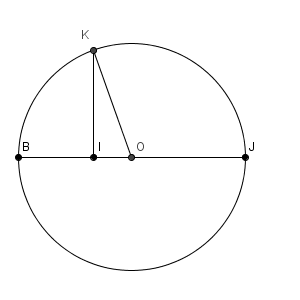
この円O の半径は、BJ の半分なので $3\sqrt{2}$ です。また、 $\mathrm{ BI }=2\sqrt{2}$ なので、 $\mathrm{ OI }=\sqrt{2}$ となるため、三平方の定理から
\begin{eqnarray}
\mathrm{ KI }
&=&
\sqrt{ (3\sqrt{2})^2 -(\sqrt{2})^2 } \\
&=&
\sqrt{ 18 -2 } \\
&=&
4
\end{eqnarray}となります。
三角錐KBDE で、三角形 DBE を底面と考えると、底面積は、冒頭で求めた通り $\displaystyle \frac{15\sqrt{7} }{4}$, 高さは $\mathrm{ KI }=4$ なので、体積は
\begin{eqnarray}
\frac{1}{3} \times \frac{15\sqrt{7} }{4} \times 4 = 5\sqrt{7}
\end{eqnarray}と求められます。
解答
ヌ:4ネノ:57





