センター試験 数学I・数学A 2017年度追試 第2問 [1] 解説
【必答問題】
問題編
問題
点 A を中心とする半径 $1$ の円がある。点 A から距離 $2$ の位置にある点 B から円 A に接線を1本引く。その接線と円 A との接点を C とし、点 D を線分 CD が円 A の直径となるようにとる。
このとき
\begin{eqnarray} & & \mathrm{ BC }=\sqrt{\myBox{ア} }, \\[5pt] & & \mathrm{ BD }=\sqrt{\myBox{イ} }, \\[5pt] & & \sin \angle \mathrm{ ABC }=\frac{\myBox{ウ} }{\myBox{エ} } \\[5pt] \end{eqnarray}である。また、 $\triangle \mathrm{ ABD }$ の外接円の半径は $\dfrac{\sqrt{\myBox{オカ} }}{\myBox{キ} }$ である。その外接円の中心を O とすると、 $\cos \angle \mathrm{ BOD } = \dfrac{\myBox{クケ} }{\myBox{コ} }$, $\dfrac{\sin \angle \mathrm{ AOC } }{\sin \angle \mathrm{ COD } } = \dfrac{\myBox{サ} }{\myBox{シ} }$ である。
考え方
よく見ると、30度や60度、120度といった角度が出てくるので、あまり計算しなくてもいろいろな値が求められます。正弦定理や余弦定理を使って解くことも大事ですが、計算が省略できるところは積極的に省略していきましょう。
最後の問題だけ、少し難易度が高いです。分母・分子の値をそれぞれ求めることなく分数の値が求められます。図形的に考える必要がありますが、センター数学の過去問をよく解いていないと、なかなか思いつかないです。
【必答問題】
解答編
問題
点 A を中心とする半径 $1$ の円がある。点 A から距離 $2$ の位置にある点 B から円 A に接線を1本引く。その接線と円 A との接点を C とし、点 D を線分 CD が円 A の直径となるようにとる。
このとき
\begin{eqnarray} & & \mathrm{ BC }=\sqrt{\myBox{ア} }, \\[5pt] & & \mathrm{ BD }=\sqrt{\myBox{イ} }, \\[5pt] & & \sin \angle \mathrm{ ABC }=\frac{\myBox{ウ} }{\myBox{エ} } \\[5pt] \end{eqnarray}である。
解説
図は次のようになっています。
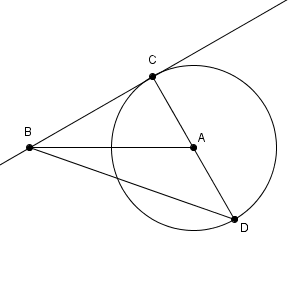
三角形 ABC は、直角三角形で、 $\mathrm{ AC }=1$, $\mathrm{ AB }=2$ なので、\[ \mathrm{ BC }=\sqrt{3} \]がわかります。また、 $\angle \mathrm{ABC}=30^{\circ}$ なので、\[ \sin\angle\mathrm{ABC}=\frac{1}{2} \]となります。
また、三角形 BCD も直角三角形で、 $\mathrm{ CD }=2$ なので、\[ \mathrm{BD}=\sqrt{\mathrm{BC}^2+\mathrm{CD}^2}=\sqrt{3+4}=\sqrt{7} \]となります。
解答
ア:3
イ:7
ウエ:12
解答編 つづき
問題
また、 $\triangle \mathrm{ ABD }$ の外接円の半径は $\dfrac{\sqrt{\myBox{オカ} }}{\myBox{キ} }$ である。
解説
$\triangle \mathrm{ ABD }$ の外接円の半径を R とします。

外接円の半径なので、正弦定理を使って解きますが、一番使いやすいところを探しましょう。そうすると、先ほど求めた BD と $\angle \mathrm{BAD}$ であることがわかります。ここは具体的に角度を求めることができますからね。
正弦定理より、
\begin{eqnarray}
2R &=& \frac{\mathrm{BD} }{\sin\angle\mathrm{BAD} } \\[5pt]
&=& \frac{\sqrt{7} }{\sin 120^{\circ} } \\[5pt]
&=& \frac{2\sqrt{7} }{\sqrt{3} } \\[5pt]
&=& \frac{2\sqrt{21} }{3} \\[5pt]
R &=& \frac{\sqrt{21} }{3} \\[5pt]
\end{eqnarray}が得られます。
解答
オカキ:213
解答編 つづき
問題
その外接円の中心を O とすると、 $\cos \angle \mathrm{ BOD } = \dfrac{\myBox{クケ} }{\myBox{コ} }$, $\dfrac{\sin \angle \mathrm{ AOC } }{\sin \angle \mathrm{ COD } } = \dfrac{\myBox{サ} }{\myBox{シ} }$ である。
解説
図は次のようになっています。

図をきれいに描かないと気づきにくいかもしれませんが、 $\angle \mathrm{BAD}=120^{\circ}$ なので、円周角の定理から $\angle \mathrm{BOD}=240^{\circ}$ (大きい方)であることがわかります。よって、小さい方は $\angle \mathrm{BOD}=120^{\circ}$ だとわかります。このことから\[ \cos \angle \mathrm{ BOD } = \cos 120^{\circ} = -\frac{1}{2} \]となります。
もしこのことに気づいていれば、先ほどの $\triangle \mathrm{ ABD }$ の外接円の半径も簡単に求められます。 BD の長さがすでに分かっていますからね。もし気づかなければ、余弦定理を使いましょう。三辺の長さが分かっているので、余弦定理が使えます。
最後の $\dfrac{\sin \angle \mathrm{ AOC } }{\sin \angle \mathrm{ COD } }$ はノーヒントだと難しいかもしれません。こうした比を使う問題は、値を直接求めなくても解けるんだろうと予想できます。センター試験の三角比の問題でよく出てくるのが、面積比を使うというものです。 $\angle \mathrm{ AOC }$ と $\angle \mathrm{ COD }$ を含む三角形で、面積比がすぐに出せそうなものを探してみます。

すると、三角形 AOC の面積と三角形 COD の面積を考えればいいことに気づきます。前者は、次のように書くことができます。\[ \frac{1}{2} \mathrm{OA}\cdot \mathrm{OC} \sin \angle \mathrm{AOC} \]また、後者は、次のように書けます。\[ \frac{1}{2} \mathrm{OD}\cdot \mathrm{OC} \sin \angle \mathrm{COD} \]両者を割ると、まず OC が消えます。また、 OA も OD も、円 O の半径なので、これらも消えます。最終的に求めたい式が出てきます。
一方、三角形 AOC の面積と三角形 COD の面積の比は、別の見方からすぐに出せます。それぞれ AC, CD を底辺と考えると、高さは同じです。なので面積比は $\dfrac{1}{2}$ であることがわかります。
以上から、\[ \dfrac{\sin \angle \mathrm{ AOC } }{\sin \angle \mathrm{ COD } } = \frac{1}{2} \]が得られます。図形的に考えないと答えにたどり着くのに時間がかかってしまいますが、思いつくのは難しいです。
解答
クケコ:-12
サシ:12





