センター試験数学I・数学A 2017年度第2問 [1] 解説

🕒 2017/01/15 🔄 2023/05/03

【必答問題】

問題編

問題

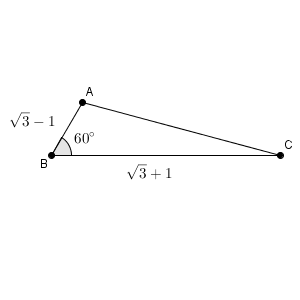
　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\sqrt{3}-1$, $\mathrm{ BC }=\sqrt{3}+1$, $\angle \mathrm{ ABC }=60^{\circ}$ とする。

(1) $\mathrm{ AC }=\sqrt{\myBox{ア} }$ であるから、 $\triangle \mathrm{ ABC }$ の外接円の半径は $\sqrt{\myBox{イ} }$ であり\[ \sin \angle \mathrm{ BAC } = \frac{\sqrt{\myBox{ウ} } +\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。ただし、$\mybox{ウ}$, $\mybox{エ}$ の解答の順序は問わない。

(2) 辺AC 上に点 D を、 $\triangle \mathrm{ ABD }$ の面積が $\displaystyle \frac{\sqrt{2} }{6}$ になるようにとるとき\[ \mathrm{ AB }\cdot \mathrm{ AD } = \frac{\myBox{カ}\sqrt{\myBox{キ} }-\myBox{ク} }{\myBox{ケ} } \]であるから、 $\displaystyle \mathrm{ AD }=\frac{\myBox{コ} }{\myBox{サ} }$ である。

考え方

図はそんなに複雑ではありません。ただ、計算の途中で有理化をする場面が多いため、計算が少し面倒です。余弦定理、正弦定理、三角形の面積を使いますが、使い方はオーソドックスです。有理化のやり方をきっちりおさえておけば、難しくはないでしょう。

【必答問題】

解答編

問題

　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=\sqrt{3}-1$, $\mathrm{ BC }=\sqrt{3}+1$, $\angle \mathrm{ ABC }=60^{\circ}$ とする。

(1) $\mathrm{ AC }=\sqrt{\myBox{ア} }$ であるから、 $\triangle \mathrm{ ABC }$ の外接円の半径は $\sqrt{\myBox{イ} }$ であり\[ \sin \angle \mathrm{ BAC } = \frac{\sqrt{\myBox{ウ} } +\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。ただし、$\mybox{ウ}$, $\mybox{エ}$ の解答の順序は問わない。

解説

余弦定理より
\begin{eqnarray} \mathrm{ AC }^2 &=& \mathrm{ AB }^2+\mathrm{ BC }^2 -2 \mathrm{ AB } \cdot \mathrm{ BC } \cos \angle \mathrm{ ABC } \\ &=& (\sqrt{3}-1)^2+(\sqrt{3}+1)^2 -2(\sqrt{3}-1)(\sqrt{3}+1) \times\frac{1}{2} \\ &=& 4-2\sqrt{3}+4+2\sqrt{3} -2 \\ &=& 6 \end{eqnarray}なので、 $\mathrm{ AC }=\sqrt{6}$ となります。

また、$\displaystyle \sin \angle \mathrm{ ABC } = \frac{\sqrt{3} }{2}$ なので、外接円の半径を R とすると、正弦定理から
\begin{eqnarray} 2R\sin \angle \mathrm{ ABC } &=& \mathrm{ AC } \\[5pt] R &=& \frac{\sqrt{6} }{\sqrt{3} } \\[5pt] &=&\sqrt{2} \end{eqnarray}と求められます。

もう一度正弦定理を使うと
\begin{eqnarray} 2R\sin \angle \mathrm{ BAC } &=& \mathrm{ BC } \\[5pt] \sin \angle \mathrm{ BAC } &=& \frac{\mathrm{ BC } }{2R} \\[5pt] &=& \frac{\sqrt{3}+1}{2\sqrt{2} } \\[5pt] &=& \frac{\sqrt{6}+\sqrt{2} }{4} \\[5pt] \end{eqnarray}と求められます。

解答

ア：6
イ：2
ウエ：6・2
オ：4

解答編つづき

問題

(2) 辺AC 上に点 D を、 $\triangle \mathrm{ ABD }$ の面積が $\displaystyle \frac{\sqrt{2} }{6}$ になるようにとるとき\[ \mathrm{ AB }\cdot \mathrm{ AD } = \frac{\myBox{カ}\sqrt{\myBox{キ} }-\myBox{ク} }{\myBox{ケ} } \]であるから、 $\displaystyle \mathrm{ AD }=\frac{\myBox{コ} }{\myBox{サ} }$ である。

解説

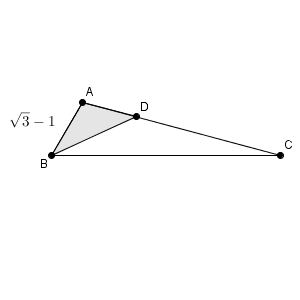
$\triangle \mathrm{ ABD }$ の面積は $\displaystyle \frac{\mathrm{ AB }\cdot\mathrm{ AD }\sin\angle \mathrm{ BAD } }{2}$ とかけます。ここで、 $\angle \mathrm{ BAD }=\angle \mathrm{ BAC }$ なので
\begin{eqnarray} \frac{\mathrm{ AB }\cdot\mathrm{ AD }\sin\angle \mathrm{ BAC } }{2} &=& \frac{\sqrt{2} }{6} \\[5pt] \mathrm{ AB }\cdot\mathrm{ AD } &=& \frac{\sqrt{2} }{6} \times \frac{2}{\sin\angle \mathrm{ BAC } } \\[5pt] \end{eqnarray}となります。この右辺を計算すると \begin{eqnarray} & & \frac{\sqrt{2} }{6} \times \frac{8}{\sqrt{6}+\sqrt{2} } \\[5pt] &=& \frac{4\sqrt{2} }{3} \times \frac{\sqrt{6}-\sqrt{2} }{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \\[5pt] &=& \frac{4\sqrt{2} }{3} \times \frac{\sqrt{6}-\sqrt{2} }{4} \\[5pt] &=& \frac{\sqrt{2}(\sqrt{6}-\sqrt{2})}{3} \\[5pt] &=& \frac{2\sqrt{3} -2}{3} \\[5pt] \end{eqnarray}となります。

$\mathrm{ AB } =\sqrt{3}-1$ なので
\begin{eqnarray} \mathrm{ AD } &=& \frac{2\sqrt{3} -2}{3} \times \frac{1}{\sqrt{3}-1} \\[5pt] &=& \frac{2(\sqrt{3}-1)}{3} \times \frac{1}{\sqrt{3}-1} \\[5pt] &=& \frac{2}{3} \\[5pt] \end{eqnarray}と求められます。