【標準】平行移動に関する作図

ここでは、平行移動に関する作図の問題を見ていきます。

平行移動に関する作図の問題

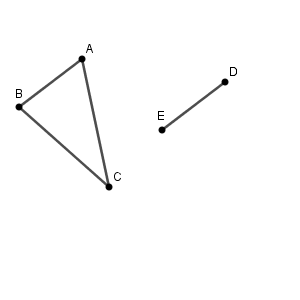
点 F が作図できればいいですね。平行移動とは、移動前と移動後で対応する点を結ぶと、どの線分も同じ長さで平行になるのでした（参考：【基本】平行移動）。つまり、点 F は、線分 CF が、線分 AD に平行で、同じ長さとなるようにすればいい、ということです。

もし、三角定規を2つ使ってもいい、という条件がついていれば、次のようにして平行な直線を引くこともできます。

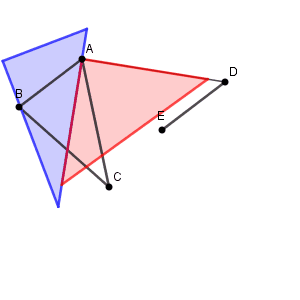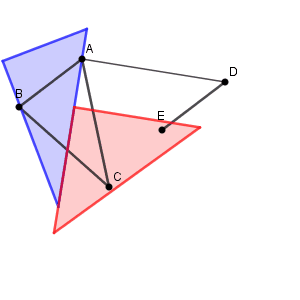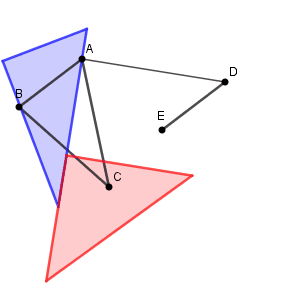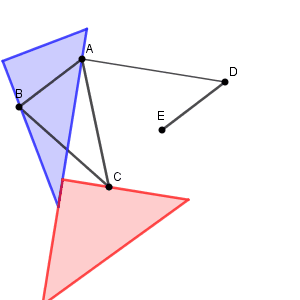
片方の三角定規の1辺を AD に合わせ、もう片方の三角定規の1辺がそれと垂直になるように合わせます。そして、 AD と合わせていた三角定規をそのままスライドしていき、点 C を通るところでストップすればいいです。こうすれば、 C を通り、 AD に平行な線がひけます。あとはコンパスで CF が AD の長さと等しくなるようにとればいいですね。

ただ、「三角定規を2つ使ってもいい」という条件がついていない場合は、定規とコンパスで作図をする必要があります。今までに学んだものを利用するなら、「垂線の垂線」を作図する方法があります。つまり、次のようにする、ということです。

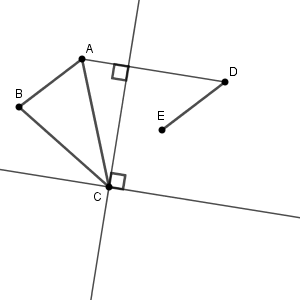
C から AD に垂線をひきます。つぎに、その垂線に垂直で、点 C を通る直線をかきます。そうすれば、 AD と平行な直線が得られます。少し大変ですが、今までに学んだ内容を組み合わせたものになります。

まず、 C から AD に垂線をひくと、次のようになります（参考：【基本】垂線の作図（直線上にない点を通る）その２）。

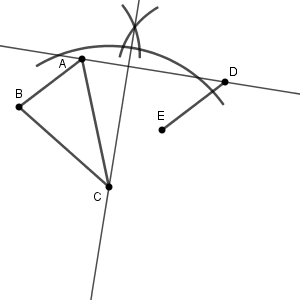
次に、この垂線に垂直で、点 C を通る直線を作図します（参考：【基本】垂線の作図（直線上の点を通る））。

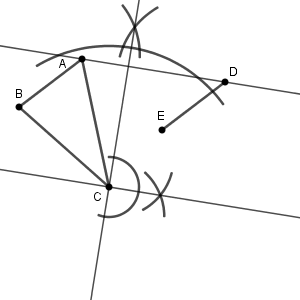
こうして、 AD に平行な直線がひけたので、あとは、 AD と CF が同じ長さになるように点 F をとればおしまいです。

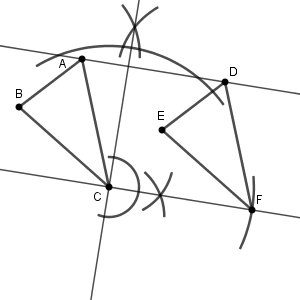
こうして、三角形 DEF が作図できます。

ひし形を利用

引き続き、同じ問題を考えます。

先ほどは、平行な直線を作図するために「垂線の垂線」を考えましたが、他にも平行な直線を作図する方法はあります。【標準】平行な線の作図の最後で見た、ひし形を利用する方法を考えてみましょう。

これは、線分 AC を一辺とするひし形を利用して、 AD に平行で点 F を通る直線を作図する方法です。

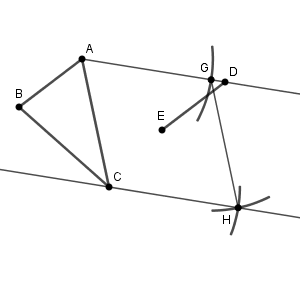
点 A を中心とした線分 AC の長さの円と、半直線 AD との交点をとります。この点を G としましょう。点 C, G から、線分 AC の長さだけ離れた点を H とすれば、四角形 ACHG はひし形となり、CH は AD と平行になります。

これより、直線 CH 上に、 $\mathrm{ CF=AD }$ となる点 F をとれば、三角形 DEF が作図できます。

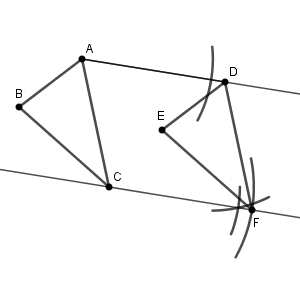
「垂線の垂線」より思いつきにくいかもしれませんが、こちらのほうが手順は少ないですね。

平行四辺形を利用

もう一度、同じ問題を考えます。

点 F が作図できたとして、四角形 ACFD がどのようになっているかをよく見てみましょう。

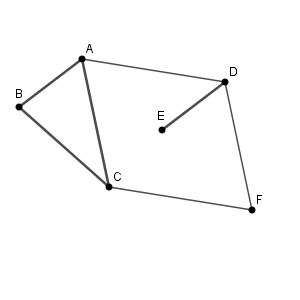
線分 AD, CF は同じ長さです。また、平行移動をしても移動前後で形や大きさは変わらないので、 $\mathrm{ AC=DF }$ です。なので、長さに関する条件を使って、 F の場所を絞ることができます。

CF が AD と同じ長さであることから、 F は、 C を中心とした半径 AD の円の円周上のどこかにあります。また、 DF が AC と同じ長さであることから、 F は、 D を中心とした半径 AC の円の円周上にもあることがわかります。

2つの円をかくと、交点が2つできます。なので、 F はこの交点のどちらかですが、片方はあきらかに変ですね。 AD と CF が平行である、という条件も満たす交点は1つだけです。このことから、次のようにして、 F を作図することができます。

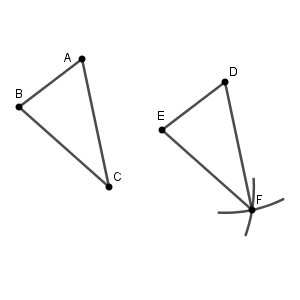
だいぶシンプルになりました。将来もう少し詳しく学びますが、この方法は四角形 ACFD が平行四辺形になるように作図していることになります。

おわりに

ここでは、平行移動した後の図形を作図する問題を見ました。平行な直線を作図するためにいろいろな方法を見ました。いろいろなやり方でできるようになっておくと、難しい問題にも応用がきくようになると思います。