🏠 Home / 中学1年 / 平面図形（中学） / 図形の移動

【標準】回転移動に関する作図（回転の中心、60度の回転）

🕒 2019/09/05 🔄 2023/05/01

ここでは、回転の中心を作図したり、60度回転移動した後の図形を作図する問題を見ていきます。

📘 目次

回転の中心の作図

例題1

下の図で、三角形 DEF は三角形 ABC をある点 O を中心として回転移動したものです。点 O を作図しなさい。

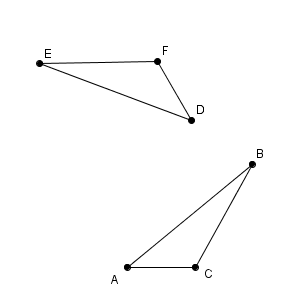
点 O はだいたいこのあたりだな、と想像がつくかもしれません。作図方法を考えるために、完成図から考えてみます。

この図を見ながら、どのようにすれば O を作図できるか考えてみましょう。

ここで注目すべきなのは、回転移動をしても、点 O からの距離は変わらない、ということです。つまり、 $\mathrm{ OA=OD }$ などが成り立つということです。2点からの距離が等しいことから、点 O は、線分 AD の垂直二等分線上にあることがわかります（参考：【基本】垂線二等分線の作図）。

このため、線分 AD, BE, CF の垂直二等分線をかいて、その交点を O とすればいいことがわかります。実際には、垂直二等分線を2本かけば交点がわかるので、かくのは3本ではなく2本で大丈夫です。作図した結果は、次のようになります。

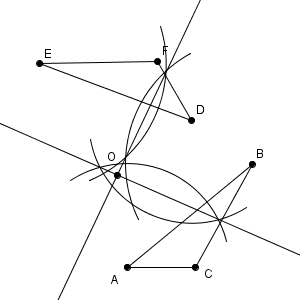
上の図では、線分 AD, BE の垂直二等分線をかいて、その交点を作図しています。

６０度の回転の作図

例題2

三角形 ABC を、点 O を中心として、反時計回りに $60^{\circ}$ 回転移動して得られる三角形 DEF を作図しなさい。

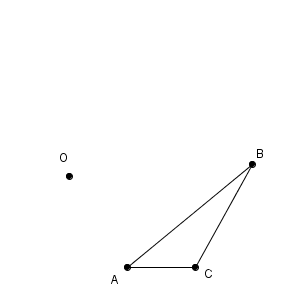
指定された角度だけ回転移動した後の図形を作図するには、普通は分度器が必要です。しかし、特定の角であれば、定規とコンパスだけで作図できます。ここでは、 $60^{\circ}$ という特別な角を利用して作図します。

まずは、1点だけを考えます。点 A が回転によって点 D に移動するので、次のような図となります。

ここで、先ほども見ましたが、 $\mathrm{ OA=OD }$ が成り立ちます。また、 $\angle \mathrm{ AOD }=60^{\circ}$ です。つまり、三角形 OAD は正三角形となります。

このことから、点 D は、点 A からも点 O からも、線分 AO と同じ長さだけ離れていることがわかります。なので、点 A, O を中心として、線分 AO の長さを半径とする円の交点が点 D となることがわかります。

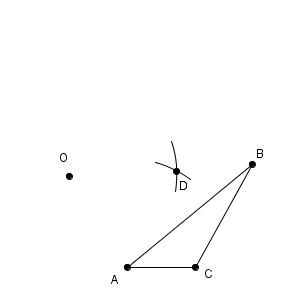
他の頂点も同様にして作図します。つまり、三角形 BOE と三角形 COF が正三角形となるように、点 E, F をとる、ということです。結果的に、三角形 DEF は次のように作図できます。

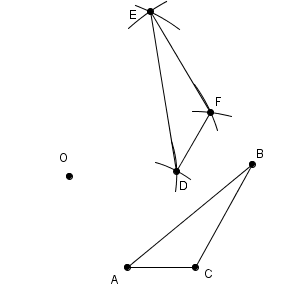
この問題では、 $60^{\circ}$ の回転であったため、正三角形を作れば、移動後の図形が得られます。しかし、これ以外の角の場合は、もっと面倒です。 $90^{\circ}$ や $45^{\circ}$ も作図できますが、 $60^{\circ}$ に比べれば大変です（三角定規の角を使っていい、という特別条件がついていれば楽になりますが）。これら以外の角だと、さらに面倒になるか、そもそも作図できないこともあります。