【基本】回転移動(東京オリンピックエンブレムを利用)
ここでは、回転移動についてみていきます。
東京オリンピックエンブレムと回転移動
ここでも、【基本】平行移動と同じように、2020年の東京オリンピック・パラリンピックのエンブレムについてみていきます。

パッと見ると、どちらのエンブレムも左右対称のように見えますが、よく見ると左側のエンブレムは左右対称にはなっていないですね。図形の上側を見ると、細長い長方形が中央に1つ、左側に2つ、右側に3つあります。なので、左右対称ではありません。この「中央が1、左が2、右が3」というのは、表彰台をあらわしている、といわれています。

さて、この「中央が1、左が2、右が3」に注目すると、エンブレムの左下にも右下にも、同じ並びを見つけることができます。

また、他の四角形についても同様に、中央の点を中心として、120度回転すれば、元の図形に戻ることがわかります。
このように、ある点を中心として、図形全体をある角度だけ回転させる移動のことを、回転移動(rotation) といいます。また、この中心のことを、回転の中心と言います。
回転移動をした図形ともとの図形とがぴったり重なるとき、この図形を回転対称な図形といいます。
回転移動の性質
【基本】平行移動では、対応する点を直線で結ぶと、互いに平行で同じ長さの線分が得られました。回転移動でも、対応する点を結ぶとどのようなことが言えるか、見てみましょう。
次のように、三角形 ABC を、点 O を中心として、反時計回りに $60^{\circ}$ 回転したものが三角形 DEF であるとします。
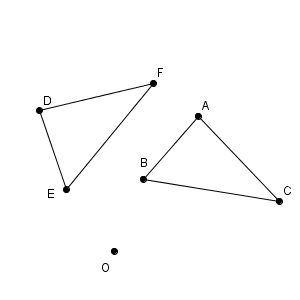
三角形全体ではなく、まずは1点だけの動きを見てみましょう。点 A が点 D へ移動するとき、点 A はどのような動きをするか考えてみます。回転なので、次のような動きになります。
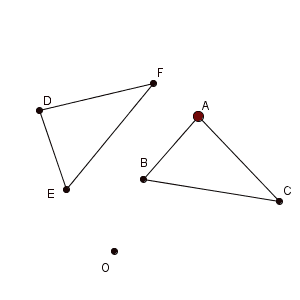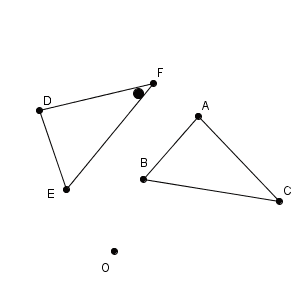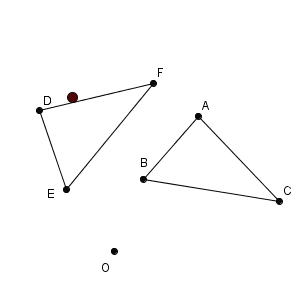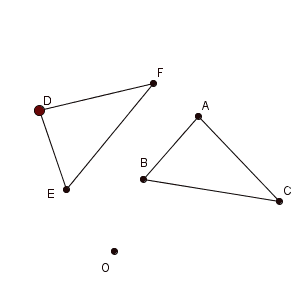
これをもとに、点 O を中心とした円(の一部)を用いて、2点 A, D を結んでみます。
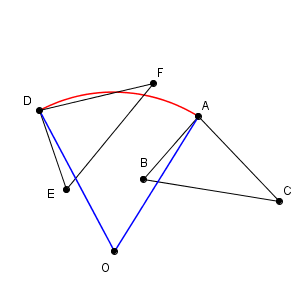
上の図から、 $\mathrm{ OA=OD }$, $\angle \mathrm{ AOD }=60^{\circ}$ がわかります。他の点も同様にすると、 $\mathrm{ OB=OE }$, $\mathrm{ OC=OF }$ もわかり、 $\angle \mathrm{ BOE }$, $\angle \mathrm{ COF }$ がどちらも $60^{\circ}$ であることがわかります。
一般に、回転移動では、対応する点は、回転の中心からの距離が等しくなります。また、対応する点と回転の中心を結んでできる角の大きさはすべて等しくなります。
例題
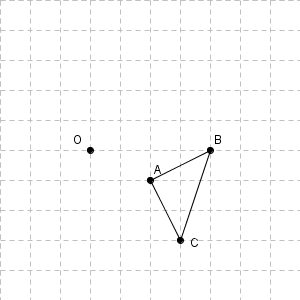
マスを利用して考えます。
例えば、点 A であれば、次の直角三角形ごと回転すると考えるとわかりやすくなります。

点 A や線分 OA がどう移動するかよりも、マスを利用して OA を斜辺とする直角三角形で考えると、移動後の点がよくわかります。他の点も同様にして、次のように三角形 DEF をかくことができます。

点対称移動
回転移動のうち、 $180^{\circ}$ 回転する場合は、特別な名前がついています。
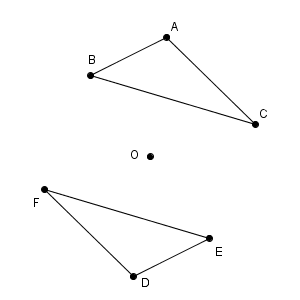
上の図では、点 O を中心として、三角形 ABC を180度回転移動したものが三角形 DEF になっています。このとき、先ほどのように、各点と回転の中心を結ぶと次のようになります。
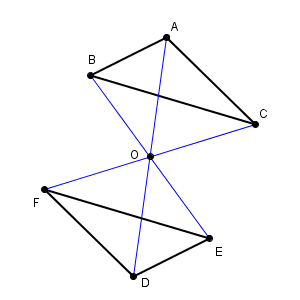
180度回転しているので、 A, D, O のような、対応する2点と回転の中心は、一直線上にあります。そのため、 A, D は、点 O についてちょうど反対側にあります。線分 AD の中点が点 O になっている、と言い換えることもできます。
このように、点 O についてひっくり返っているように見え、他の回転移動とは少し違っています。 $180$ 度だけ回転移動させることを、点対称移動といいます。
点対称移動をした図形ともとの図形とがぴったり重なるとき、この図形を点対称な図形といいます。
おわりに
ここでは、回転移動について見てきました。対応する点は回転の中心からの距離が等しくなること、対応する点と回転の中心を結んでできる角の大きさがすべて等しくなることをおさえておきましょう。





