【標準】チェバの定理とメネラウスの定理
ここでは、チェバの定理やメネラウスの定理を使った問題を見ていきます。
チェバの定理やメネラウスの定理を使った例題
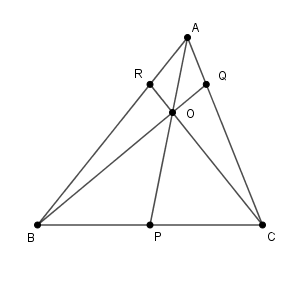
(1) $\mathrm{BP:PC}$ を求めなさい。
(2) $\mathrm{\triangle OBP:\triangle ABC}$ を求めなさい。
角度に関する情報がまったくなく、線分の比を考えたいので、チェバの定理やメネラウスの定理が使えるのではないか、と予想できます。
まず、(1)の $\mathrm{BP:PC}$ を考えます。わかっている線分の比や求めたい線分の比を見ながら考えると、チェバの定理が使えるとわかります。

$\triangle \mathrm{ABC}$ と点 $\mathrm{O}$ に対して、チェバの定理を使うと
\begin{eqnarray}
\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} &=& 1 \\[5pt]
\frac{1}{3} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{3}{1} &=& 1 \\[5pt]
\frac{\mathrm{BP}}{\mathrm{PC}} &=& 1 \\[5pt]
\end{eqnarray}となります。よって、比は\[ \mathrm{BP} : \mathrm{PC}=1:1 \]と求められます。
チェバの定理やメネラウスの定理を使った例題の続き
続いて、(2)を考えましょう。

(1) $\mathrm{BP:PC}$ を求めなさい。
(2) $\mathrm{\triangle OBP:\triangle ABC}$ を求めなさい。
面積比を求めます。長さは何もわからないので面積を求めることはできません。ここまでで辺の比が登場しているので、面積比も辺の比を利用して考えていくことにしましょう。
まず、(1)で求めたように、 $\mathrm{BP:PC}=1:1$ です。なので、 $\triangle \mathrm{ABP}:\triangle \mathrm{ABC}=1:2$ です。さらに $\triangle \mathrm{OBP}$ を考えるには、 $\mathrm{AO:OP}$ がわかればいいです。
$\mathrm{AO:OP}$ はそのままではわかりませんが、これを含む形でチェバの定理やメネラウスの定理が使えないか考えてみます。

チェバの定理を使う場合は、 $\triangle \mathrm{ABP}$ の内部に点がないとダメなので、チェバの定理は難しそうです。一方、メネラウスの定理の場合、 $\mathrm{AP}$ を含む三角形で、 $\mathrm{O}$ が辺と直線の交点となるようなものを考えると、三角形 $\mathrm{ABP}$ と直線 $\mathrm{CR}$ に対してメネラウスの定理を使えばいいことがわかります。
こうして
\begin{eqnarray}
\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BC}}{\mathrm{CP}} \cdot \frac{\mathrm{PO}}{\mathrm{OA}} &=& 1 \\[5pt]
\frac{1}{3} \cdot \frac{2}{1} \cdot \frac{\mathrm{PO}}{\mathrm{OA}} &=& 1 \\[5pt]
\frac{\mathrm{PO}}{\mathrm{OA}} &=& \frac{3}{2}
\end{eqnarray}となることがわかり、 $\mathrm{PO:OA}=3:2$ となることがわかります。これより、 $\mathrm{AP:OP}=5:3$ なので
\begin{eqnarray}
\triangle \mathrm{OBP}
&=&
\frac{3}{5} \times \triangle \mathrm{ABP} \\[5pt]
&=&
\frac{3}{5} \times \frac{1}{2} \times \triangle \mathrm{ABC} \\[5pt]
&=&
\frac{3}{10} \times \triangle \mathrm{ABC} \\[5pt]
\end{eqnarray}となることがわかるので、\[ \triangle \mathrm{OBP}:\triangle \mathrm{ABC}=3:10 \]と求められます。
ちなみに、面積比は他の方法でも求めることができます。

$\mathrm{AR:AB}=\mathrm{AQ:AC}=1:4$ なので、 $\triangle \mathrm{ARQ}$ と $\triangle \mathrm{ABC}$ は相似で、相似比は $1:4$ です。なので、 $\mathrm{RQ}$ と $\mathrm{BC}$ は平行です。そのため、 $\triangle \mathrm{OQR}$ と $\triangle \mathrm{OBC}$ は相似で、相似比は $1:4$ です。
このことから、 $\mathrm{RO:OC}=1:4$ なので
\begin{eqnarray}
\triangle \mathrm{OBP}
&=&
\frac{1}{2}\times \triangle \mathrm{OBC} \\[5pt]
&=&
\frac{1}{2}\times \frac{4}{5}\times \triangle \mathrm{RBC} \\[5pt]
&=&
\frac{1}{2}\times \frac{4}{5}\times \frac{3}{4}\times \triangle \mathrm{ABC} \\[5pt]
&=&
\frac{3}{10} \times \triangle \mathrm{ABC} \\[5pt]
\end{eqnarray}となるため、\[ \triangle \mathrm{OBP}:\triangle \mathrm{ABC}=3:10 \]と求められます。
この問題では、$\mathrm{AR:RB}$ と $\mathrm{AQ:QC}$ が同じなので相似であることが使えますが、同じでない場合は上のような相似を利用する方法は使えません。しかし、チェバの定理やメネラウスの定理を使う方法なら解けます。より汎用的な方法だと言えるでしょう。
おわりに
ここでは、チェバの定理やメネラウスの定理を使った問題を見ました。図形の問題では、いろんなアプローチで考えることができますが、辺の比や面積比を求めるときには、チェバの定理やメネラウスの定理が使えないか、考えてみるようにしましょう。





