【標準】おうぎ形と正方形の面積
ここでは、おうぎ形と正方形が組み合わさった面積を求める問題を見ていきます。
おうぎ形と正方形の面積その1
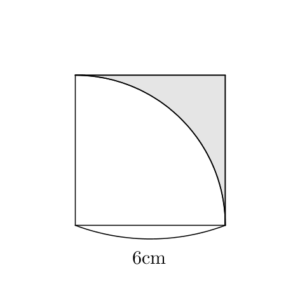
このような部分の面積を直接求める公式はないので、今までに学んだものを組み合わせて求めます。
外側の正方形のうち、内側にあるおうぎ形を除いた部分が色のついた部分なので、正方形の面積からおうぎ形の面積を引けば求められますね。おうぎ形の半径は、正方形の一辺の長さと等しく、 $6\mathrm{ cm }$ です。また、中心角は、正方形の1つの角と等しいので、 $90^{\circ}$ です。以上から、面積は
\begin{eqnarray}
& &
6^2-6^2\times\pi\times\dfrac{90}{360} \\
&=&
36-9\pi \\
\end{eqnarray}なので、 $(36-9\pi) \mathrm{ cm }^2$ となります。
また、中学入試の勉強をしたことがある人なら、次のような部分の面積を求める問題を見たことがあるかもしれません。
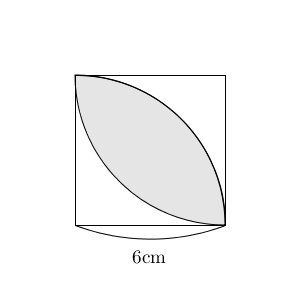
これは、正方形から、先ほど求めた面積を2つ分引いて求めることができます。つまり
\begin{eqnarray}
& &
6^2-2\times(36-9\pi) \\[5pt]
&=&
36-72+18\pi \\[5pt]
&=&
18\pi-36 \\[5pt]
\end{eqnarray}から、 $(18\pi-36) \mathrm{ cm }^2$ と求められます。
この答えをよく見てみると、 $18\pi-36$ のうち、 $36$ は正方形の面積を表していると考えられます。では $18\pi$ は何かというと、円の面積は $36\pi \mathrm{ cm }^2$ なのだから、これは半円の面積だと考えることができます。なぜ、半円から正方形の面積を引けば求められるかは、次のように考えるといいでしょう。
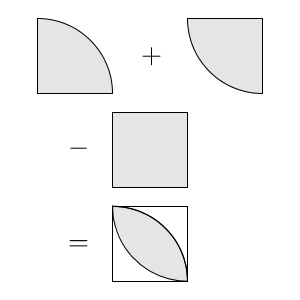
中心角が90度のおうぎ形2つを合わせると、重なる部分が2回足され、他の部分は1回ずつ足されます。なので、正方形を引けば、重なった部分の面積だけが出てきます。この求め方は、自力で思いつくのは難しいかもしれませんが、このように組み合わせて面積を求める問題もあります。
おうぎ形と正方形の面積その2
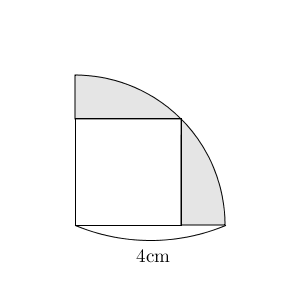
おうぎ形の半径と中心角はすぐにわかりますが、正方形の一辺の長さがすぐにはわかりません。なので、正方形の面積をどう求めればいいのかを考えることになります。
正方形の大きさを知る手掛かりは、辺を見ていてもわかりません。おうぎ形と正方形とは、おうぎ形の弧の上にある1点を共有していますが、この点が正方形の大きさを決めているものとなります。
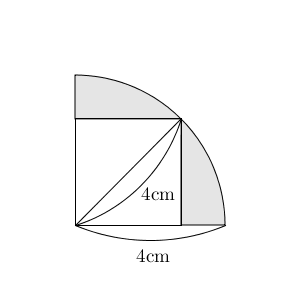
そのため、この問題では、正方形の1辺の長さはすぐにはわかりませんが、対角線の長さはわかります。対角線の長さがわかると、これは、次のように4つの直角二等辺三角形があると考えれば面積を求めることができます。
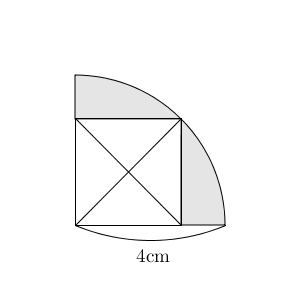
こうして、色のついた部分の面積は
\begin{eqnarray}
& &
4^2\pi\times\frac{90}{360}-2\times2\times\frac{1}{2}\times 4 \\[5pt]
&=&
4\pi-8 \\[5pt]
\end{eqnarray}なので、 $(4\pi-8)\mathrm{ cm }^2$ となることがわかります。
なお、ひし形や正方形のような、対角線が垂直に交わっている図形は、対角線の長さを用いて面積を求めることができます。
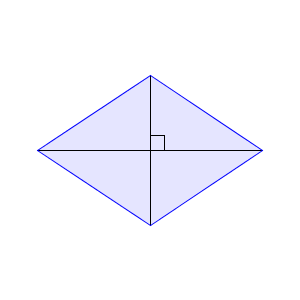
この場合、次のようにすると、平行四辺形ができます。
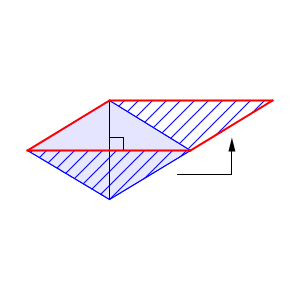
この平行四辺形の底辺は、もとの図形の対角線の1本そのままで、高さはもう1本の対角線の半分の長さです。なので、2本の対角線の長さを掛けて2で割れば、面積を求めることができます。
先ほどの問題であれば、対角線の長さが $4\mathrm{ cm }$ だったので、 $\dfrac{4^2}{2}=8$ とすぐに計算できます。直角三角形4つ分と考えてもいいですが、「対角線の積の半分」と求めると、より速く求められるので、使えるようになっておくと役立つでしょう。
おわりに
ここでは、おうぎ形と正方形を組み合わせた図形の面積を求める問題を見てきました。
面積を求めるためには、線分の長さや角度を知る必要がありますが、これらを図から読み取らないといけない場合もあります。また、公式を組み合わせないと、求めたい面積が計算できないこともあります。





