【基本】おうぎ形などの面積

ここでは、三角形や四角形の面積について簡単に振り返った後に、円やおうぎ形の面積の求め方を見ます。

面積

図形の大きさや広さを表したいときに使うものが面積(area) です。

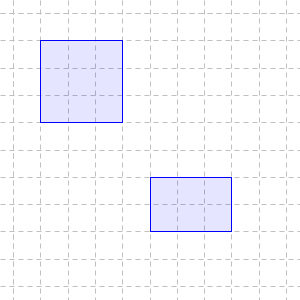
基準の単位がcmの場合を考えると、縦1cm、横1cmの正方形がいくつあるかで面積を表します。この場合の面積の単位は、 $\mathrm{cm}^2$ です。上の図で1目盛りを1cmとすると、正方形の面積は $9 \mathrm{cm}^2$ であり、長方形の面積は $6 \mathrm{cm}^2$ となります。

長方形の面積は、縦×横、正方形の面積は、一辺×一辺で求められます。

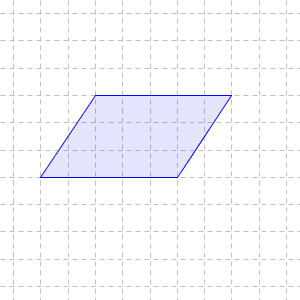
平行四辺形の場合は、一辺が1cmの正方形がいくつ分かがわかりづらいですね。斜めの線が出てくるとやっかいなので、次のように変形して考えます。

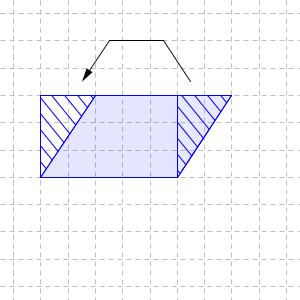
こうすると、長方形の面積を求めることになるので、 $15 \mathrm{cm}^2$ だとわかります。こうして長方形の面積に帰着して求めることができます。

平行四辺形の面積は、底辺×高さで求められます。底辺と高さは、垂直である点に注意しましょう。

三角形の面積

次のような直角三角形の面積を考えてみましょう。

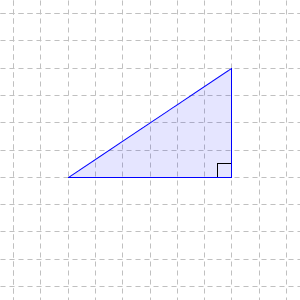
これも直接求めることは難しいですが、同じものを2つ使うと、求められるようになります。

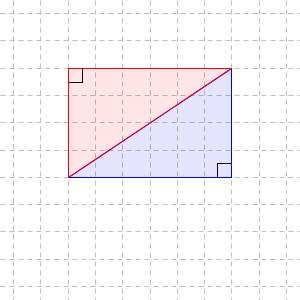
同じ三角形をひっくり返して組み合わせると、この直角三角形の面積は長方形の面積の半分だ、ということがわかります。こうして、 $12 \mathrm{cm}^2$ と求められます。

直角三角形以外の三角形でも、2つ使うと平行四辺形ができるので、同じように求められます。三角形の面積は、底辺×高さ÷2 で求められます。

台形も似たような考え方で求められます。

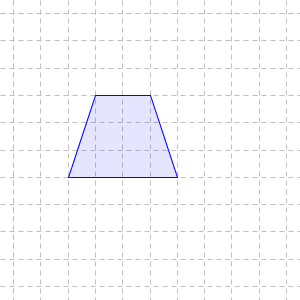
三角形のときのように、同じものを2つ使って、次のようにしてみましょう。

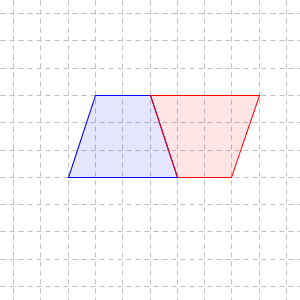
これも、平行四辺形の半分だとわかります。平行四辺形の底辺は、台形の平行な2辺の和と一致しています。これに高さを掛けて2で割れば、台形の面積となります。上の図では、 $9 \mathrm{cm}^2$ と求められます。

台形の辺のうち、平行な2辺を、上底と下底と呼びます。どちらがどちらを指すかは決まっていませんが、長い方を下底ということが多いです。台形の面積は、「（上底+下底）×高さ÷2」で求められます。

円の面積

円の面積は、三角形や四角形の面積とは異なり、簡単には求められません。ざっくりとした説明になってしまいますが、以下のようにして考えます。

まず、円をピザのように切って、下のようにかみ合わせるようにして並べます。

変形後の図で、弧の長さ（青い部分の長さ）の和は、もとの円の円周の長さに等しいですね。そのため、変形後の図の上側も下側も、長さは、もとの円周の長さの半分に等しいことがわかります。

切り方をどんどん細くしていきましょう。おうぎ形の中心角を小さくしていく、と言い換えることもできます。そうすると、細長いおうぎ形がたくさんでき、かみ合わせた図は長方形に近づいていきます。

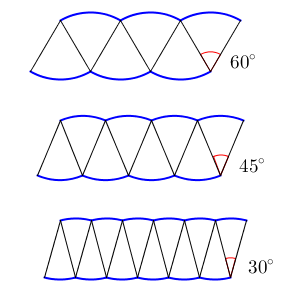
こうして、最終的には、縦がもとの円の半径、横が円周の半分の長方形に近づいていきます。円周の半分ということは、直径×円周率の半分だから、半径×円周率ですね。なので、円の面積は、「半径×半径×円周率」となります。

半径を $r$ cm とすると、円の面積は $\pi r^2 \mathrm{cm}^2$ となります。円周を求めるときと同じく、面積を求めるときにも、円周率は $\pi$ を使います。問題文で指定がない限り、3.14 を使って計算することはありません。

おうぎ形の面積

【基本】円とおうぎ形では、おうぎ形の弧の長さを求めるときに、円周を分割して求めました。中心角が $60^{\circ}$ だったら、1周 $360^{\circ}$ に対する割合を考えればいいのでした。

おうぎ形の面積も同様に考えます。

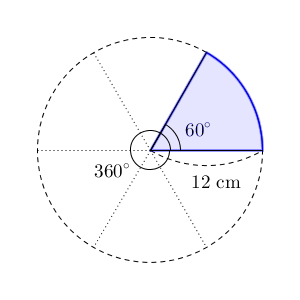
上の図は、半径 $12$ cmで中心角が $60^{\circ}$ のおうぎ形です。この面積は、円の面積の $\dfrac{60}{360}$ 倍なので、\[ 12^2\pi \times \frac{60}{360}=24\pi \]なので、 $24\mathrm{cm}^2$ となることがわかります。

おうぎ形の弧の長さと面積

最後に、おうぎ形の弧の長さと面積を、一般的な形でまとめておきましょう。

どちらも、円の場合に対して、360度に対する中心角の割合を掛けると求められます。

おわりに

ここでは、いろいろな面積の求め方を振り返った後、おうぎ形の面積を見てきました。公式を使うだけの問題が出ることは少なく、どのように組み合わせて求めるかを自分で考える問題がほとんどです。いろいろな問題を解いて練習しましょう。