🏠 Home / 中学1年 / 平面図形（中学） / 平面図形の基礎

【応用】おうぎ形と正方形の面積

🕒 2019/07/06 🔄 2023/05/01

ここでは、おうぎ形と正方形が組み合わさった、面積を求める問題を見ていきます。ここで見る問題は、将来、もっと簡単に解く方法を学びますが、ここでは、今までに学んだことだけを用いて解いていきます。

📘 目次

おうぎ形と正方形の面積その１

例題1

次の図は、正方形とおうぎ形を組み合わせた図形です。色のついた部分の面積を求めなさい。

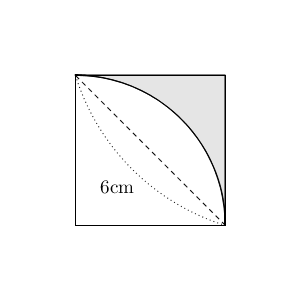
【標準】おうぎ形と正方形の面積の前半で見た問題とよく似ていますが、わかっている長さが違っています。リンク先では正方形の一辺の長さがわかっていましたが、この問題では対角線の長さがわかっています。

面積は、正方形の面積からおうぎ形の面積を引いて求めればいいですね。ただ、一辺の長さや半径を求めるのは難しいです。

先ほどのリンク先の後半では、ひし形や正方形の面積を、対角線の長さから求める方法もあることを見ました。対角線が垂直に交わっていれば、次のように変形すればいいのでした。

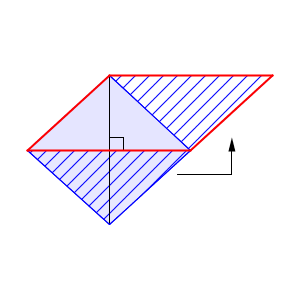
このことを使えば、正方形の面積は出せますね。\[ 6\times 6\times \dfrac{1}{2}=18 \]なので、 $18\mathrm{ cm }^2$ と求められます。

問題はおうぎ形の面積です。この例題では、半径×半径×円周率× $\dfrac{1}{4}$ を計算できればいいのですが、半径を求めるのは難しいです。しかし、面積を求めるには、半径ではなく、「半径×半径」がわかればいいんですね。そして、これはもうすでに求めています。この問題では、半径×半径とは、正方形の面積と同じです。半径はわからなくても、半径×半径がわかることもあるんですね。

こうして、おうぎ形の面積は、\[18\times\pi\times\frac{1}{4}=\frac{9}{2}\pi\]で求めることができるので、この問題の答えは、 $\left(18-\dfrac{9}{2}\pi\right)\mathrm{ cm }^2$ となります。

半径ではなく、半径×半径がわかればいい、と考えるのがポイントです。

おうぎ形と正方形の面積その２

例題2

次の図は、正方形とおうぎ形を組み合わせた図形です。色のついた部分の面積を求めなさい。

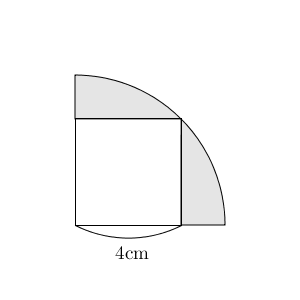
これは、【標準】おうぎ形と正方形の面積の後半で見た問題とよく似ていますが、これも先ほどと同じように、わかっている長さが違います。リンク先では半径がわかっていますが、この問題では正方形の一辺の長さがわかっています。

正方形の面積は、 $16\mathrm{ cm }^2$ だとすぐにわかりますが、問題はおうぎ形の面積ですね。面積は、半径×半径×円周率× $\dfrac{1}{4}$ で求められますが、半径を求めるのは難しそうです。

おうぎ形と正方形の大きさの関係を見ると、正方形の対角線の長さとおうぎ形の半径が同じですね。それは、次のようにかくとわかりやすいです。

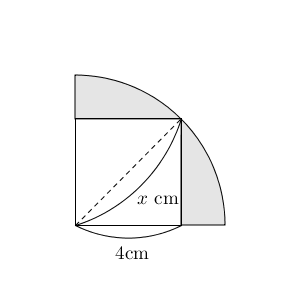
先ほどの例題では、おうぎ形の半径はわからなかったけど、半径×半径を求めることはできました。そのときに、正方形の面積を使いましたね。上の図でも、同じような考え方を応用して求めてみましょう。

おうぎ形の半径を $x\mathrm{ cm }$ とすると、 $x^2$ が求められれば面積が求められますね。この半径は、正方形の対角線とも同じです。また、対角線の長さを使って正方形の面積を表すと、 $\dfrac{x^2}{2}\mathrm{ cm }^2$ となります。この値は、 $16\mathrm{ cm }^2$ となるのだから、\[ x^2=16\times 2=32 \]と求められます。こうして、半径×半径が求められます。

こうして、おうぎ形の面積は、\[ x^2\times\pi\times\frac{1}{4}=8\pi \]と求められます。よって、色のついた部分の面積は、 $(8\pi-16)\mathrm{ cm }^2$ と求められます。

先ほどの例題と同じように、半径×半径を求めるのがポイントですが、求め方は先ほどよりも難しくなっています。