【応用】二次方程式の解がある範囲内に存在

ここでは、二次方程式の解がある範囲内に存在することを示す問題を考えていきます。

例題1

二次方程式の解は、解の公式を使えば求められますね。なので、解を求めてそれが $0$ と $1$ の間にあることを言えば、OKなはずです。係数を見ると少しイヤな予感がしますが、まずは解を求めてみましょう。

解の公式より、解は次のように求められます。
\begin{eqnarray} x &=& \frac{-(\sqrt{7}-1) \pm \sqrt{(\sqrt{7}-1)^2+4(\sqrt{2}+1)}}{2} \\[5pt] &=& \frac{1-\sqrt{7} \pm \sqrt{12-2\sqrt{7}+4\sqrt{2}}}{2} \end{eqnarray}この分子は、どれくらいの値なのか、なかなか考えづらいですね。イヤな予感が当たってしまいました。

この方針でもがんばればできますが、以下では、もう少し楽に示す方法を考えます。

似た問題として、【応用】二次方程式が実数解を持つ条件（ともにある範囲内）を見てみましょう。リンク先の問題では、「解が $0$ と $2$ の間にあるとき」を考えました。このようなケースを考えるために、二次関数のグラフを利用しました。

ここでも、この考え方を応用してみましょう。二次方程式の左辺を $f(x)$ とします。つまり、次のように置きます。\[ f(x)=x^2+(\sqrt{7}-1)x-(\sqrt{2}+1) \]このとき、 $x=0$ とすると\[ f(0)=-(\sqrt{2}+1) \lt 0 \]となるので、 $y=f(x)$ のグラフは、 $y$ 軸と負の部分で交わります。では、 $0$ と $1$ の間に解があるというのは、グラフはほかにどんな条件を満たしていればいいでしょうか。

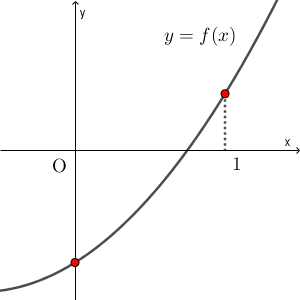
$x=1$ のときの値に注目すればいいですね。 $f(1)$ が正であれば、上の図のように、 $0$ と $1$ の間でグラフは $x$ 軸を横切るので、必ず $0$ と $1$ の間に解があることがわかります。実際に確かめてみると
\begin{eqnarray} f(1) &=& 1+(\sqrt{7}-1)-(\sqrt{2}+1) \\[5pt] &=& \sqrt{7}-\sqrt{2}-1 \\[5pt] &\gt& \sqrt{2.5^2}-\sqrt{1.5^2}-1 \\[5pt] &=& 2.5-1.5-1=0 \\[5pt] \end{eqnarray}となり、たしかに $f(1)\gt 0$ となることがわかりました。

こうして、 $f(0)\lt 0$ と $f(1)\gt 0$ から、 $y=f(x)$ のグラフは $0$ と $1$ の間で $x$ 軸と交わることがわかるので、 $f(x)=0$ は $0$ と $1$ の間に解をもつことがわかります。

ちなみに、グラフは次のようになっています。

表面上は二次方程式の問題ですが、二次関数や二次不等式で学んだ考え方を応用して解くことができます。

例題2

すごく抽象的で答えにくい問題ですね。例題1の前半で考えたように、展開して解の公式を使って、というやり方も考えられますが、ちょっと大変そうです。

これも、例題1の後半で見たような解き方ができます。左辺を $f(x)$ とおきましょう。つまり、次のようにします。\[ f(x) = (x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a) \]

ここで、 $x=a$ とすると3つのうち2つの項が消えます。 $a\lt b\lt c$ であることも使うと
\begin{eqnarray} f(a) &=& (a-b)(a-c) \gt 0 \end{eqnarray}となることがわかります。同様にすると、\[ f(b)=(b-c)(b-a)\lt 0 \]であり、\[ f(c)=(c-a)(c-b) \gt 0 \]であることもわかります。

$f(a), f(b), f(c)$ は、順番に、正、負、正だとわかりました。このことから、 $y=f(x)$ のグラフは $a$ と $b$ の間で $x$ 軸と交わり、 $b$ と $c$ との間でも $x$ 軸と交わることがわかります。こうして、 $f(x)=0$ は、 $a$ と $b$ の間に解があり、 $b$ と $c$ の間にも解があることがわかります。

おわりに

ここでは、二次方程式の解がある範囲内に存在することを示す問題を見てきました。二次関数のグラフがどのようになっているかを考えることで、解を直接考えなくてもよくなる、というところがポイントでした。二次方程式の問題に見えても、二次関数や二次不等式で学んだことを利用して解くこともあるので、よく理解しておきましょう。