【標準】二次不等式を満たす整数

🕒 2023/07/11 🔄 2023/07/13

ここでは、二次不等式を満たす整数に関する問題を見ていきます。

📘 目次

例題

$2x^2+x+a \lt 0$ を満たす整数がちょうど3個存在するような、 $a$ の範囲を求めなさい。

例えば、 $a=-1$ なら\[ 2x^2+x-1=(2x-1)(x+1) \]です。なので、これが負になる範囲は $-1\lt x\lt \dfrac{1}{2}$ だから、不等式を満たす整数は $x=0$ の1個だけ、となります。これが3個になる場合を考えましょう、という問題です。

個数しかわからないというのは少し不便です。ただ、よく考えると、個数が3個なら、どの整数3個なのかは、特定することができます。

二次不等式を解くときには二次関数のグラフを利用しました。そこで、 $f(x)=2x^2+x+a$ とおいて、 $y=f(x)$ のグラフについて考えてみましょう。

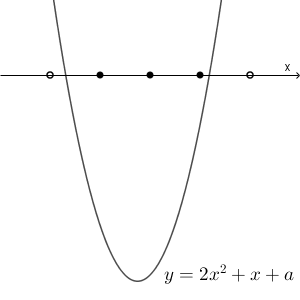
$a$ の値によって $y=2x^2+x+a$ のグラフの上下位置は変わりますが、二次不等式を満たす整数が3個であるということは、上のような状況になっているはずです。放物線の軸に近い3つの点（黒丸）ではグラフは $x$ 軸より下で、それ以外の点（白丸）では $x$ 軸より上にある、という状況です。つまり、軸に近い3つの点が二次不等式の解に対応します。

平方完成をすると、\[ 2\left(x+\frac{1}{4}\right)^2 +a-\frac{1}{8} \]となるので、軸は $x=-\dfrac{1}{4}$ です。 $x$ 座標が整数である点のうち、この軸に近い $x$ 軸上の点は、近い方から $(0,0)$, $(-1,0)$, $(1,0)$ です。また、これらの次に近い点は、$(-2,0)$ です。

以上から、グラフは次のようになっていないといけません。

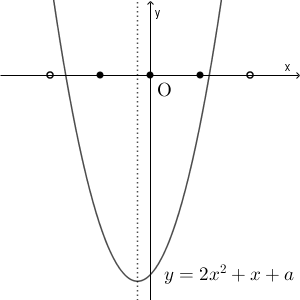
まず、$f(1)\lt 0$ という条件が必要です。これを満たしていると、 $x=-1,0,1$ の3つが問題文にある不等式を満たします。一方、 $f(-2)\geqq 0$ という条件も必要です。 $f(-2)$ は $0$ でもいいことに注意しましょう。これら2つの条件を満たせば、先ほどの3つ以外の整数は、問題文の不等式を満たさないことがわかります。

$f(1)\lt 0$ を解くと、 $3+a\lt 0$ より $a\lt -3$ が得られます。 $f(-2)\geqq 0$ を解くと、$6+a\geqq 0$ より、$a\geqq -6$ が得られます。以上から、\[ -6 \leqq a \lt -3 \]が答えだとわかります。

ちなみに、 $a=-3$ のときは、グラフは次のようになります。

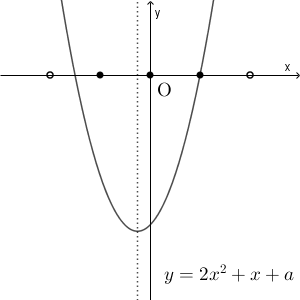
このとき、 $f(1)=0$ となっています。 $x=1$ は $f(x)\lt 0$ の解ではないので、この場合は整数解は3個にはなりません。$a$ がこれより少しでも小さければ $f(1)\lt 0$ となります。

一方、 $a=-6$ のときはグラフはこのようになります。

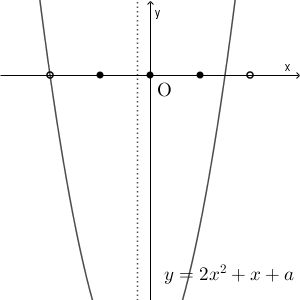
この場合は $f(-2)=0$ となります。この場合、 $x=-2$ は $f(x)\lt 0$ の解ではないので、 $f(x)\lt 0$ の整数解は $x=-1,0,1$ の3個となります。 $a$ がこれより少しでも小さくなると、 $f(-2)\lt 0$ となってしまい、整数解の個数は3個ではなくなってしまいます。

整数解の個数を考える場合は、ギリギリの箇所（今の例だと、$x=1$ や $x=-2$ の箇所）に注意して考えましょう。ちょっとしたことで、等号の有無などが変わってきます。