【応用】二次方程式が実数解を持つ条件（ともに正）

【標準】二次方程式が実数解を持つ範囲の応用として、ここでは、「二次方程式が正の実数解を持つ範囲」を求める問題を考えます。「正の」がついただけですが、考えることはいろいろ増えてしまいます。

例題

「正の」というのがやっかいです。もし「異なる2つの実数解」だけであれば、【標準】二次方程式が実数解を持つ範囲で見たように、「判別式が正となる条件」を考えればいいんでしたね。そのため、まずは次の条件が必要です。\[ (-2a)^2-4(a+6) \gt 0 \]これを解くと、
\begin{eqnarray} 4a^2-4a-24 & \gt & 0 \\ a^2-a-6 & \gt & 0 \\ (a+2)(a-3) & \gt & 0 \\ \end{eqnarray}なので、下のグラフから、 $a\lt -2, a\gt 3$ という範囲が求められます。

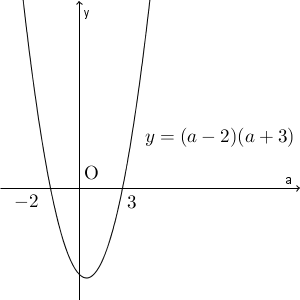
軸に注目

ただ、上で求めた条件は、 $x^2-2ax+a+6=0$ が異なる2つの実数解を持つ、というだけなんですね。その実数解が正かどうかはわかりません。 $y=x^2-2ax+a+6$ のグラフは次のようにいろんなパターンがありえます。

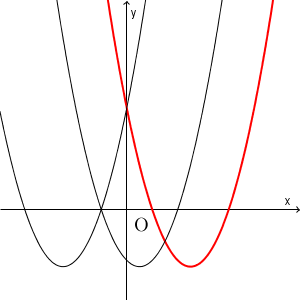
（心の声：赤いグラフを考えたいので、黒いグラフを除外する条件を考えたい）

「放物線が x 軸と2点で交わっている」というケースには、 x 座標が、両方正、片方だけ正、両方負、などのパターンも含まれています。これらの中で、両方正になるパターンだけ抜き出すにはどうすればいいでしょう。

もちろん、放物線の交点を求めてそれが正になる条件を求める、という方法でもいいのですが、もっと計算を減らす方法で考えます。放物線を特徴づけるものの1つに、「放物線の軸」がありましたね。軸に注目してみましょう。

放物線と x 座標との交点の x 座標が両方正になるには、少なくとも軸が y 軸より右に来ないといけない、というのはグラフからわかります。 x 軸より左にあった場合は、必ず片方の解は負になってしまいますからね。

\begin{eqnarray} x^2-2ax+a+6 = (x-a)^2-a^2+a+6 \end{eqnarray} なので、この放物線の軸は直線 $x=a$ だから、 $a\gt 0$ でないといけないことが分かります。

この条件を満たす場合、「両方負」のケースは完全に除外されます。下のグラフで言うと、破線のグラフが候補からはずれる、ということですね。

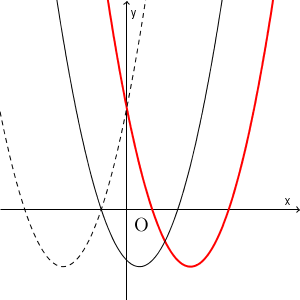
y軸との交点に注目

しかし、まだ、「片方が正で片方が負」というケースが含まれてしまいます。これを除外するにはどうすればいいでしょう。「両方正」の場合には成り立つが「片方正、片方負」の場合には成り立たない条件、を図を見て考えてみましょう。

そうすると、違いは、「y 軸とどこで交わっているか」であることがわかります。 y 軸と正の部分で交わっている、という条件も満たせば、「両方正」となります。 y 軸との交点は $a+6$ なので、これが正となるのは $a\gt -6$ のときですね。

放物線の軸が y 軸より右で、 y 軸と正の部分で交わっているとき、放物線と x 軸とは、原点や x 軸の負の部分で交わることができないことがわかります。よって、今まで考えた次の3つの条件：

• 判別式が正
• 放物線の軸が y 軸より右にある
• 放物線が y 軸と正の部分で交わる

をすべて満たすものが答えとなります。上で求めた通り、これらに対応する条件は次の通りでした。

• $a\lt -2$ または $a\gt 3$
• $a\gt 0$
• $a\gt -6$

この3つすべてを満たすものは、 $a\gt 3$ なので、これが答えとなります。

ちなみに、「判別式が正」と「放物線が y 軸と正の部分で交わる」の2つの条件だけでは、「 x 座標との交点の x 座標が両方正」とは言えません。両方負の場合も含まれてしまいます。なので、「放物線の軸が y 軸より右にある」という条件も必要です。上の3つの条件すべてが必要です。

おわりに

ここでは、「二次方程式が異なる2つの正の実数解を持つ」ための条件を考えました。上で考えたのと同じように考えると、次のように一般的に書くことができます。

上で考えた例題は、「 $k=0$ のとき」と考えることができます。

3つの条件のうち、どれか1つでも満たさないものがあると、不必要なグラフが紛れ込んでしまうので注意しましょう。

なお、 a が負のときは、3つ目の条件が $f(k)\lt 0$ となります。また、「実数解がともに負」の場合は、2つ目の条件が「放物線の軸が $x=k$ より左にある」に変わります。