🏠 Home / 数学I / 二次関数 / 二次不等式

【応用】二次方程式が実数解を持つ条件（片方正、片方負）

🕒 2016/09/12 🔄 2023/05/01

ここでは、【応用】二次方程式が実数解を持つ条件（ともに正）に関連して、実数解の片方が正、片方が負になる場合を考えます。また、最後に、片方がある値 k より大きく、もう片方が k より小さい場合をまとめます。

「ともに正」のときと、少し条件が異なります。

📘 目次

例題

二次方程式 $x^2+ax+a^2-3=0$ が異なる2つの実数解を持ち、片方の解が正でもう片方が負になるとき、 a の範囲を求めなさい。

$f(x)=x^2+ax+a^2-3$ とおいて、 $y=f(x)$ のグラフを考えていきます。

【応用】二次方程式が実数解を持つ条件（ともに正）のときと同じように、「判別式」「放物線の軸」「$f(k)$ の符号」という点で考えてみましょう。

まず、「異なる2つの実数解を持つ」ので、「判別式が正」という条件を満たさないといけないことが分かります。

次に、「放物線の軸」についてはどうでしょうか。「実数解が片方正、片方負」となるためには、放物線の軸については特にこれといった条件は必要なさそうです。下のグラフを見てみましょう。

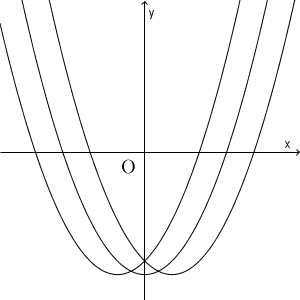
どれも、放物線と x 軸との交点の x 座標が「片方正、片方負」となっています。しかし、一番左は放物線の軸が y 軸よりも左、真ん中は y 軸と一致、右側は放物線は軸が y 軸より右となっています。つまり、「片方正、片方負」となるために、放物線の軸が満たさないといけない条件はない、ということです。

最後に、「$f(k)$ の符号」、ここでは「$f(0)$ の符号」について考えましょう。グラフをいろいろかいてみると、放物線と x 軸との交点の x 座標が「片方正、片方負」となるには、「$f(0)$ が負」という条件を満たせばいいことがわかります。

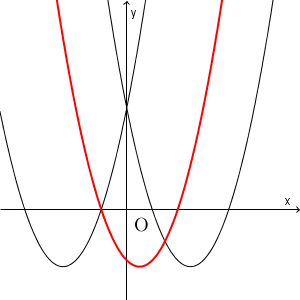
下に凸の放物線の場合、グラフの左側はどんどん上に向かっていくし、右側も上に向かっていきます。なので、 $x=0$ のときの y 座標が負なら、 x 座標が正の部分と負の部分で、それぞれ1か所ずつ、放物線と x 軸が交わることが分かります。

ということは、「下に凸で $f(0)$ が負」なら、放物線は x 軸と異なる2点で必ず交わることもわかります。つまり、「放物線が x 軸と2点で交わる＝判別式が正」という条件は、「下に凸で $f(0)$ が負」ならいつでも成り立つ、ということです。

以上から、考えるべき条件は、「 $f(0)$ が負」だけになります。 $f(0)=a^2-3$ なのでこれが負になるのは、\[ -\sqrt{3}\lt a \lt \sqrt{3} \]となります。これが答えです。

本当に判別式について考えなくていいのか

「下に凸で $f(0)$ が負」なら「判別式が正」はいつでも成り立つ、と書きましたが、本当にそうなのかを確認しておきましょう。

$f(x)=ax^2+bx+c \ (a\gt 0)$ とします。平方完成すると次のようになります。\[ f(x)=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a} \]ここで、放物線 $y=f(x)$ は下に凸だから、頂点の $y$ 座標は $f(0)$ 以下です。なので、 $f(0)\lt 0$ なら、頂点の $y$ 座標も負になることが分かります。上の平方完成した式で考えると\[ -\frac{b^2-4ac}{4a} \lt 0 \]ということです。これに $-4a$ という負の値を掛けると\[ b^2-4ac \gt 0 \]となります。この左辺は判別式そのものです。

以上から、 $a\gt 0,\ f(0)\lt 0$ なら、常に判別式が正になることが分かります。なので、これらの条件を満たせば、判別式が正になる条件は考えなくてもいい、ということになります。