【応用】チェバの定理とメネラウスの定理
ここでは、チェバの定理やメネラウスの定理の少し見た目が違うバージョンを見ていきます。
少し見た目が違うチェバの定理
【基本】チェバの定理 でも見た通り、チェバの定理とは、下のような図で $\dfrac{\mathrm{AR}}{\mathrm{RB}} \cdot \dfrac{\mathrm{BP}}{\mathrm{PC}} \cdot \dfrac{\mathrm{CQ}}{\mathrm{QA}} = 1$ が成り立つという内容でした。
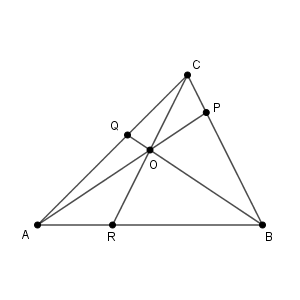
これは、「点 $\mathrm{O}$ をとって、直線 $\mathrm{AO,BO,CO}$ を引いて、辺との交点 $\mathrm{P,Q,R}$ をとる」と考えてもいいですし、「辺上に点 $\mathrm{P,Q,R}$ をとって、向かいにある頂点と結ぶと1点で交わった」と考えてもいいです。どちらで考えてもいいのですが、上の図では、$\mathrm{O}$ は三角形の内部の点だと仮定していました。
実は、点 $\mathrm{O}$ は三角形の外にあってもかまいません。辺やその延長線上にない場合、同じように、頂点 $\mathrm{A, B, C}$ に対して、点 $\mathrm{O}$ とその頂点を通る直線を引き、対辺(もしくはその延長線)と交わる点を $\mathrm{P, Q, R}$ とすると、 $\dfrac{\mathrm{AR}}{\mathrm{RB}} \cdot \dfrac{\mathrm{BP}}{\mathrm{PC}} \cdot \dfrac{\mathrm{CQ}}{\mathrm{QA}} = 1$ が成り立ちます。
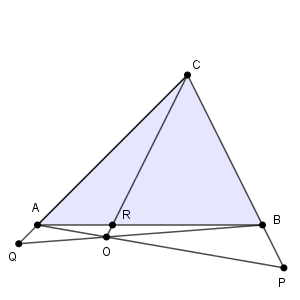
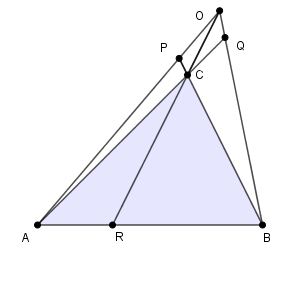
3直線の交点が三角形の内部にあるときと比べて、少し図がわかりにくいですね。2つ目の例は、どちらも $\mathrm{C}$ 側の延長線上にある場合で、1つ目の例はどちらも $\mathrm{C}$ 側ではない延長線上にある場合となっています。これらの場合も含めて、チェバの定理ということがあります。
証明は、交点が三角形の内部にあるときと同じように、面積比を使って示せます。
内部にあることを限定しないバージョンのチェバの定理は、次のような内容になります。
このとき、次の等式が成り立つ。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]
ちなみに、点 $\mathrm{O}$ が辺やその延長線の上にあるときは、 $\dfrac{\mathrm{AR}}{\mathrm{RB}} \cdot \dfrac{\mathrm{BP}}{\mathrm{PC}} \cdot \dfrac{\mathrm{CQ}}{\mathrm{QA}}$ に出てくるどれかの線分が $0$ になってしまいます。
例えば、辺 $\mathrm{AB}$ 上に点 $\mathrm{O}$ があるとすると、直線 $\mathrm{AO}$, $\mathrm{BC}$ の交点 $\mathrm{P}$ は $\mathrm{B}$ と一致してしまい、 $\mathrm{BP}$ の長さが $0$ となってしまいます。
そのため、点 $\mathrm{O}$ が辺やその延長線の上にあるケースは除外しています。
少し見た目が違うメネラウスの定理
【基本】メネラウスの定理 でも見た通り、メネラウスの定理とは、下のような図で $\dfrac{\mathrm{AR}}{\mathrm{RB}} \cdot \dfrac{\mathrm{BP}}{\mathrm{PC}} \cdot \dfrac{\mathrm{CQ}}{\mathrm{QA}} = 1$ が成り立つという内容でした。
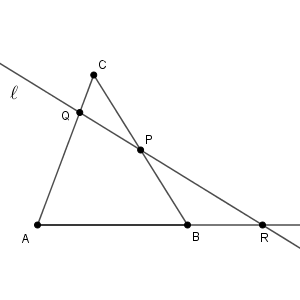
実は、ここに出てくる直線 $\ell$ は、辺もしくはその延長線と交わればいい(ただし、頂点は除く)ので、次のような場合でも構いません。

直線 $\ell$ がどの辺とも交わっていない場合です。この場合も、定理に出てくる積は $1$ になります。この図を見て「メネラウスの定理が使える」と気づくのは少し難しいですね。
証明は、リンク先にある、2つの辺と交わる場合と同じです。点の位置は異なりますが、証明の内容はそのまま使えます。
メネラウスの定理の内容をよく読むと、上の2つのどちらのケースにも対応していることがわかります。なので、チェバの定理のときのように内容を書き直す必要はありません。
3点がどこにあるか
ここまでで、少し見た目の違うチェバの定理とメネラウスの定理を見てきましたが、他にどんなパターンがあるでしょうか。3点($\mathrm{P,Q,R}$)がどこにあるかに注目して、もう一度見てみましょう。

上の図はチェバの定理が使える図ですが、このときの3点はすべて辺の上にあります。

上の図はメネラウスの定理が使える図です。このときは、3点のうち、2点が辺の上、残りの1点は辺の延長線上にあります。


上の2つは最初の画像とは少し見た目が違いますが、チェバの定理が使える図です。どちらも、「3点のうち、1点が辺の上、残り2点は辺の延長線上」となっています。

これは少し見た目の違うメネラウスの定理です。辺の上にある点はなく、3点すべてが辺の延長線上にあります。
試行錯誤してみると、三角形 $\mathrm{ABC}$ があったときに
- 直線 $\mathrm{AO,BO,CO}$ と辺または辺の延長線上との交点 $\mathrm{P,Q,R}$
- 辺または辺の延長線上とある直線 $\ell$ との交点 $\mathrm{P,Q,R}$
おわりに
ここでは、少し見た目の違うチェバの定理やメネラウスの定理を見てきました。ここで見た内容は、チェバの定理の逆やメネラウスの定理の逆にもつながっていく内容です。





