【基本】文字を使った式の表し方（数字と文字の積）

ここでは、文字を使った式の表し方のルールを見ていきます。数字と文字の積の表し方について見ていきます。

文字を使った式の復習

【基本】文字を使った式で表そうで見た内容を、簡単に振り返りましょう。

次のように、マッチ棒を使って正方形を作っていったときに、正方形を10個作るのに必要なマッチ棒の数を考えました。縦の長さがマッチ棒1本の長さです。

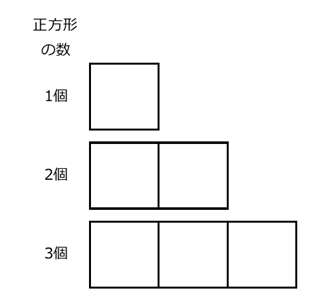
正方形が少ない場合に、直接数え挙げて、規則性を考えました。数えた結果、正方形が1つ増えるごとに、マッチ棒は3本増えることがわかります。このことは、次のように正方形を分解すればわかりやすいのでした。

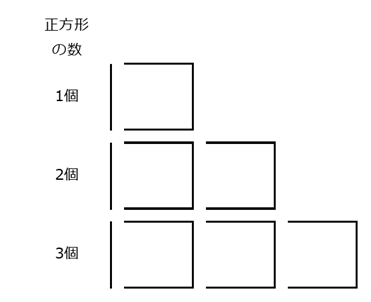
このことから、左端の「｜」と、右側にある複数の「コ」に分けて数えればいいのでしたね。正方形を10個作るには、「コ」の形を10個作ればいいので、マッチ棒の数は、\[ 1+3\times 10=31 \]だから、31本必要だということがわかります。

正方形の個数が変わっても、マッチ棒の数は同じように計算できます。このことを一般的に表すために、文字を使って表現するのでしたね。正方形を $x$ 個作りたいとします。このときに必要なマッチ棒の数は、先ほどの「10」の部分を $x$ に置き換えて\[ 1+3\times x \]と書くことができます。こうして、正方形の個数からマッチ棒の本数を求める方法を、一般的に表すことができます。この $x$ は、 $1,2,3$ や $10$ といった、いろいろな数を表すもの、いろいろな数の代わりに使われているものです。

こうして文字で表すことで、複雑なものも簡潔に表せるようになっていきます。

文字を使った式での積の表し方（数字と文字の積）

さて、文字を使った式では、いくつかのルールがあります。ここからはそのルールを紹介していきます。

まず、先ほどの式\[ 1+3\times x \]ですが、このように、文字の混じった乗法では、 $\times$ の記号を省略します。つまり、この式は、\[ 1+3x \]と書きます。

また、文字と数との積では、数のほうを前に書きます。つまり、 $a\times 2$ は、 $2a$ と書きます。 $a2$ とは書かないので注意しましょう。

なお、式の途中にある＋や－の記号は省略できません。なので、 $1+3x$ を $13x$ とは書きません。後者は $13$ と $x$ との積なので、前者とは意味が違ってしまいます。

$\times$ の記号を省略すること、省略するときには数字のほうを前にすることに注意して表します。

(1)は、 $10a$ となります。 $a10$ ではありません。

(2)は、 $120m+150n$ となります。 $m,n$ どちらの $\times$ も省略します。

文字を使った式での積の表し方（1や負の数との積）

先ほど、数字と文字を掛ける場合は、掛け算の記号 $\times$ を省略することを見ました。さらに、1や負の数を掛ける場合には、次のようにします。

まず、 $1$ との積は、 $1$ そのものを省略します。つまり、 $1\times x$ は $1x$ とは書かずに、 $x$ だけにします。

また、 $(-3)\times t$ というように、負の数と文字を掛ける場合は、カッコも省略します。つまり、 $(-3)t$ ではなく、 $-3t$ と書きます。 $(-1)\times t$ の場合は、 $-t$ となります。

ちなみに、 $1$ が省略できるのは、 $1$ との積の場合だけです。例えば、 $0.1\times a$ は、 $0.1a$ となります。 $0.a$ とはなりません。

$1$ との積の場合は $1$ を省略すること、負の数を掛ける場合はカッコも省略することに注意して表します。

(1)は、 $3-2m$ となります。

(2)は、 $-x+y$ となります。 $x,y$ どちらの $\times$ も省略します。また、 $1$ やカッコも省略します。

(3)は、 $1000-111s$ となります。 $111s$ にある $1$ は省略しません。 $1$ との積ではなく、 $111$ との積だからです。

なお、式の途中にある＋や－の記号は省略できませんが、式の一番はじめが ＋ のときは省略します。つまり、 $+x+y$ なら $x+y$ と書きます。

おわりに

ここでは、文字を使って積を表すときのルールを見てきました。他にもありますが、まず数字と文字の積について表せるようになりましょう。