【基本】正負の数の乗法（移動で考える）

🕒 2019/04/17 🔄 2023/05/01

ここでは、負の数の掛け算について見ていきます。移動を使って考えていきます。

📘 目次

正の数と正の数の積を移動で考えてみよう

正の数と負の数との積や、負の数同士の積は、【基本】正負の数の乗法（規則性から考える）で見ましたが、ここでは、移動を用いてもう一度考えてみましょう。なお、掛け算のことを乗法と言い、掛け算の結果のことを積というのでしたね。

負の数の掛け算を考えるため、小学校の算数で、掛け算が出てきた場面を思い出してみましょう。「皿の上にみかんが3個あって、皿が4枚あるとすると、みかんは全部で何個あるか」みたいなときに使いました。ただ、このような「モノの個数」を使って考えても、負の数は扱いにくそうです。みかんがマイナス3個ある、といわれても意味が分かりません。なので、別の例を考えましょう。

掛け算は、「速さ×時間＝距離」という場面でも使いました。時間であれば、マイナスの値を考えることもできますね。例えば、マイナス3時間というのは、今より3時間前だと考えることができます。速さがマイナスというのは、移動する向きが反対だと考えればいいですね。例えば、右に移動することをプラスで表すとすると、左への移動はマイナスで表すことができます。

なので、この「速さ×時間＝距離」を使って、負の数の掛け算を考えてみることにしましょう。

次のように、左右に伸びる道があって、ある人が右向きに時速4kmで歩いているとします。右への移動をプラスで表すことにしましょう。数直線を意識しています。

今いる地点を基準にすると、3時間後にはどこにいるかを考えてみます。これは、算数でやりましたが、\[ 4\times3=12 \]なので、右に12km移動したところにいることがわかります。

右へ時速4km動くということを、符号をつけて表せば、 $+4$ とかけます。また、今を基準にすると、3時間後は、 $+3$ と表せます。なので、符号をつけて表せば、上の式は\[ (+4)\times(+3)=+12 \]とも書けますね。

こうした書き方をもとにして、負の数を掛けた場合を考えてみましょう。

正の数と負の数との積

先ほどの、「ある人が右向きに時速4kmで歩いている」ケースを考えます。この人は、2時間前はどこにいたでしょうか。時間がたてば、どんどん右に移動するのだから、時間をさかのぼれば、今よりも左にいることがわかるでしょう。

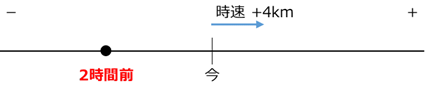
この2時間で $4\times 2=8$ kmだけ歩いているはずなので、2時間前は、今より8km左の地点にいることがわかります。

これらを、符号をつけた数で表してみましょう。速さは、先ほどと同じで $+4$ と書けます。また、今より2時間前は、 $-2$ となります。今より8km左の地点は、 $-8$ と書けるので、式で表せば、\[ (+4)\times(-2)=-8 \]となります。

数字の部分を掛けて、マイナスをつけたものになっていますね。

負の数と正の数との積

今度は、移動する向きを変えましょう。「ある人が左向きに時速4kmで歩いている」ケースを考えてみましょう。この人は、3時間後はどこにいるでしょうか。今度は、時間がたてば、どんどん左に移動していきます。

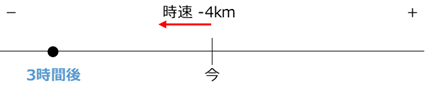
3時間で $4\times 3=12$ kmだけ歩いているはずなので、3時間前は、今より12km左の地点にいることがわかります。

これらを、符号をつけた数で表してみましょう。今、右への移動をプラスで表しているので、左への移動はマイナスとなります。なので、速さは、 $-4$ と書けます。また、今より3時間後は、 $+3$ となります。今より12km左の地点は、 $-12$ と書けるので、式で表せば、\[ (-4)\times(+3)=-12 \]となります。

今回も、数字の部分を掛けて、マイナスをつけたものになっていますね。