【基本】一次式の項とまとめ方

ここでは、式の計算のうち、一次式の項のまとめ方について見ていきます。

同じ文字が複数ある式

【導入】文字式の計算でも簡単に触れましたが、ここから、式の計算方法について見ていきます。が、その前に、具体的にどのようなことをするのかを例を使って見ていきます。

次のような式があるとしましょう。\[ 3x+7x \]これは、 $3$ と $x$ の積と、 $7$ と $x$ の積を足し合わせたものですね。この $x$ という文字は、実際には何かの数字を表しているのでした（参考：【基本】文字を使った式で表そう）。

例えば、 $x=5$ なら\[ 3\times 5 + 7\times 5 \]のことだし、 $x=-2.4$ なら\[ 3\times (-2.4)+7\times (-2.4) \]のことです。これらの計算は、直接計算することもできますが、【標準】正負の数と分配法則で見たように、分配法則を使って計算することもできます。分配法則を使って $x=-2.4$ のときを計算すると
\begin{eqnarray} & & 3\times (-2.4) +7\times (-2.4) \\[5pt] &=& (3+7)\times (-2.4) \\[5pt] &=& 10\times (-2.4) \\[5pt] &=& -24 \end{eqnarray}となります。それぞれを計算するよりも楽になります。

これを、代入する前、つまり、 $3x+7x$ の状態で、同じようにまとめてみましょう。 $x$ が数字を表していると思って先ほどと同じように計算すれば、
\begin{eqnarray} & & 3x +7x \\[5pt] &=& 3\times x +7\times x \\[5pt] &=& (3+7)\times x \\[5pt] &=& 10\times x \\[5pt] &=& 10x \end{eqnarray}とまとめることができます。

図で考えてみると、これは、次のように考えられます。

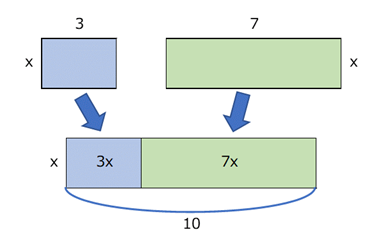
横の長さが $3$ と $7$ で、縦の長さがどちらも $x$ の長方形の面積を考えた場合、2つの面積の和は、2つをくっつけた長方形の面積と同じです。なので、 $3x+7x$ と $10x$ が同じであることがわかるでしょう。

$x$ に値を代入するときも、 $3x+7x$ に代入するときは2回代入することになりますが、 $10x$ なら1回で済みます。その後の計算も楽です。なので、まとめられるものはまとめるようにした方がいいですね。このように、同じ文字をまとめたりして式を簡単な形にすることを、「式を計算する」といいます。

項と係数

先ほど、 $3x+7x$ という式を見ました。この式の $3x$ や $7x$ のように、 $+$ で結ばれているものを項(term) といいます。例えば、 $1+3x$ なら、項は $1$, $3x$ です。 $2a+4b$ なら、項は $2a$, $4b$ です。

$2a-4b$ のような引き算の場合は、次のように、和の形にしてから考えます。
\begin{eqnarray} & & 2a-4b \\[5pt] &=& 2a+(-4b) \\[5pt] \end{eqnarray}これより、項は、 $2a$, $-4b$ となります。

項は、文字を含まないものと含むものがあります。含むもののうち、数字の部分を係数(coefficient) といいます。例えば、 $7x$ なら、係数は $7$ です。 $-4b$ なら、係数は $-4$ となります。なお、 $a$ や $-a$ の場合は、係数は $1$, $-1$ となります。

これらの用語を使うと、先ほど $3x+7x$ を $10x$ とした変形は、次のように言葉で説明することができます：「同じ文字を含む項は、係数を足し合わせて1つの項にまとめることができる」。

しばらくの間は、1つの式に含まれる文字は1種類で、文字の部分に累乗を用いない文字式の計算を扱っていきます。このような式を、一次式といいます。当面は文字が1つだけの一次式を扱うので、 $s+t$ とか $ax+5$ とか $x^2+x+1$ のような式は出てきません。

例題

冒頭で見たように、 $3x+7x$ という式では、どちらの項も $x$ を含んでいるため、まとめることができるのでした。係数同士を足して $(3+7)x=10x$ とできるのでした。これは、分配法則を使った変形でしたね。

分配法則は引き算でも成り立つので、 $3x-7x$ は、係数同士を引いて $(3-7)x=-4x$ と計算することができます。

これらをもとに、次の問題を考えてみましょう。

(1)は、 $a$ を含む2つの項の和なので、係数同士を足して\[ 2a+5a=(2+5)a=7a \]となります。

(2)は、 $y$ を含む2つの項の差なので、係数同士の差を計算します。 $y$ の係数は $1$ なので、\[ y-4y=(1-4)y=-3y \]と計算できます。

おわりに

ここでは、一次式の項と係数、そして、項のまとめ方を見ました。項のまとめ方は、一次式の加法や減法で、もう少し練習します。