【基本】一次式と数の乗法

ここでは、一次式と数の乗法について見ていきます。

一次式と数の乗法（項が１つ）

【基本】一次式の加法や減法では、一次式同士の足し算や引き算を見ました。ここでは、乗法について見ていきます。

次の式を見てみましょう。\[ 3x\times 4 \]これは、次のように考えます。もともと $3x$ は $3\times x$ のことでした。掛け算は、計算する順番を変えても結果が変わらないので、数字の部分同士を掛けてまとめることができます。つまり、
\begin{eqnarray} & & 3x\times 4 \\[5pt] &=& 3\times x \times 4 \\[5pt] &=& 3\times 4 \times x \\[5pt] &=& 12x \\[5pt] \end{eqnarray}となります。ここでは説明のためにくどく書いていますが、慣れてくれば、数字の部分だけを掛けて計算すればOKです。

負の符号がついているときも、数字の部分の計算をします。\[ (-2a)\times (-5) \]の場合は、数字の部分、 $-2$ と $-5$ を掛けて、\[ (-2a)\times (-5)=10a \]と計算します。

一次式と数の乗法（項が複数）

先ほどは、項が1つだけの場合を見ましたが、ここでは、次のように項が複数あるときの積を考えてみましょう。\[ 3(2x+1) \]

カッコのある式と数との積を計算するには、【基本】正負の数と分配法則で見たように、分配法則を使いました。この分配法則は、文字が含まれている式でも同じように使えます。次の長方形の面積で考えてみるとわかりやすいでしょう。

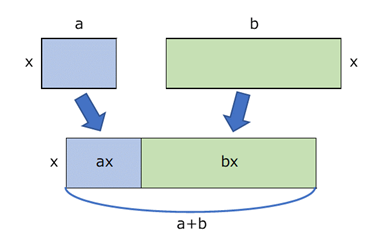
これは、縦が $x$ で横が $(a+b)$ の長方形の面積は $x(a+b)$ と書けます（カッコをつけないと、 $x$ は $a$ にしか掛からないので、カッコが必要です）。これを、2つの長方形がくっついたものだと考えれば、 $ax+bx$ とも書けますね。分配法則は文字を含んでいる式でも使うことができます。

このことから、先ほどの式 $3(2x+1)$ は次のように計算します。
\begin{eqnarray} & & 3(2x+1) \\[5pt] &=& 3\times 2x + 3\times 1 \\[5pt] &=& 6x+3 \\[5pt] \end{eqnarray}このようになります。

マイナスが絡んでくると、符号を間違いやすくなります。 $(2x-1)\times(-3)$ であれば、次のように計算します。
\begin{eqnarray} & & (2x-1) \times (-3) \\[5pt] &=& 2x\times(-3) -1\times (-3) \\[5pt] &=& -6x +3 \\[5pt] \end{eqnarray}となります。 $-1$ と $-3$ を掛けないといけないことに注意しましょう。

また、次のような場合も注意が必要です。\[ -(a+2) \]これも符号を間違いやすいです。これは、 $-1$ と $a+2$ との積だと考えて
\begin{eqnarray} & & -(a+2) \\[5pt] &=& -1\times a-1\times 2 \\[5pt] &=& -a-2 \end{eqnarray}となります。カッコ内の $+2$ の符号を変え忘れてしまう間違いが多いので注意しましょう。

例題

(1)は、数字の部分を掛けてまとめます。\[ 7x\times(-3)=-21x \]となります。

(2)は、符号に注意しましょう。\[ (-2)\times(-6a)=(-2)\times(-6)\times a=12a \]となります。

(3)は、分配法則を使います。 $2$ を $-3$ にも掛けることを忘れないようにしましょう。
\begin{eqnarray} & & 2(4m-3) \\[5pt] &=& 2\times 4m-2\times 3 \\[5pt] &=& 8m-6 \\[5pt] \end{eqnarray}となります。

(4)も分配法則を使って計算します。符号にも注意しながら、次のように計算します。
\begin{eqnarray} & & \left(-\dfrac{1}{3}x-\dfrac{1}{4}\right)\times(-12) \\[5pt] &=& -\dfrac{1}{3}x \times (-12)-\dfrac{1}{4}\times(-12) \\[5pt] &=& 4x+3 \\[5pt] \end{eqnarray}となります。分配法則の使い方、符号、分数の計算、と間違いやすい点が複数混じっていて大変ですが、慣れないうちは、1つ1つゆっくり確かめながら計算しましょう。

おわりに

ここでは、一次式と数の乗法について見てきました。分配法則を使う場面では、掛け忘れ、符号の間違いなどが発生しやすいので注意して計算しましょう。