【基本】正負の数と分配法則

ここでは、負の数を含んだ計算で、分配法則について見ていきます。

正の数と分配法則

次のような、長方形の面積を考えてみましょう。

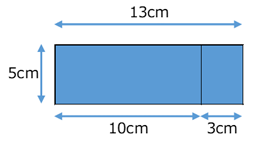
縦が $5$ cm、横が $13$ cm です。左端から $10$ cmのところに線が入っているとします。

外側の長方形の面積は、 $5\times13$ (㎠)で求められます。また、これは内側2つの長方形の面積の和とも等しいですね。つまり、\[ 5\times10+5\times3 \]と等しいことがわかります。

このことから、\[ 5\times(10+3)=5\times10+5\times3 \]が成り立ちます。また、同じように考えれば、\[ (10+3)\times5=10\times5+3\times5 \]が成り立つこともわかるでしょう。

算数のときも見たかもしれませんが、一般的に次のような式が成り立ちます。

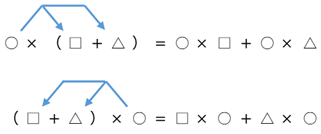
カッコの中が引き算の場合にも、同じような式が成り立ちます。次の図を見てみましょう。

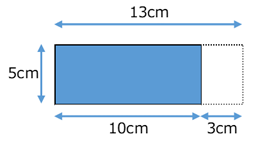
外側の長方形の面積から右側の長方形の面積を引く、と考えると、\[ 5\times(13-3)=5\times13-5\times3 \]が成り立つことがわかります。

これらの計算の性質を、分配法則(distributive property) といいます。

これを使えば、計算が楽になることがあります。例えば、\[ \left(\frac{2}{9}+\frac{5}{6}\right)\times 36 \]を計算する場合、普通はカッコの中を計算しますが、通分をしなくてはいけませんね。しかし、分配法則を使えば、\[
\frac{2}{9}\times36+\frac{5}{6}\times36=8+30=38 \]となり、分数の和の計算をしなくてすむので、少し楽になります。

正負の数と分配法則

先ほど、\[ 5\times(10+3)=5\times10+5\times3 \]というような、分配法則が成り立つことを見ましたが、これは負の数に対しても成り立ちます。負の数の掛け算は符号が変わるだけなので、 $5$ を $-5$ に変えた場合、両辺とも答えは $-65$ となります。つまり、\[ (-5)\times(10+3)=(-5)\times10+(-5)\times3 \]が成り立ちます。

一般的に、正の数でも負の数でも、次の式が成り立ちます。
\begin{eqnarray} \bigcirc\times(\square+\triangle) &=& \bigcirc\times\square+\bigcirc\times\triangle \\[5pt] (\square+\triangle)\times\bigcirc &=& \square\times\bigcirc+\triangle\times\bigcirc \\[5pt] \end{eqnarray}つまり、分配法則が成り立つ、ということですね。

負の数の場合、符号を間違いやすいので注意しましょう。\[ (-5)\times(10-3) \]の場合であれば、\[ (-5)\times 10 +(-5)\times(-3) \]と計算したり、\[ (-5)\times 10 -(-5)\times3 \]と計算します。 $(-5)$ と $-3$ を掛けるときの符号に注意しましょう。

例題

正の数と負の数が混じった計算で、分配法則を使ってみましょう。

(1)は、 $24$ をカッコ内の数にそれぞれ掛けて
\begin{eqnarray} & & 24 \times\left(\dfrac{1}{12}-\dfrac{5}{8}\right) \\[5pt] &=& 24 \times\dfrac{1}{12}-24 \times\dfrac{5}{8} \\[5pt] &=& 2-15 \\[5pt] &=& -13 \\[5pt] \end{eqnarray}となります。もちろん、カッコ内を計算して $24\times \left(-\dfrac{13}{24}\right)$ と求めても構いません。

(2)は、後ろの $-36$ をカッコ内の数にそれぞれ掛けて
\begin{eqnarray} & & \left(-\dfrac{5}{9}+\dfrac{1}{2}\right)\times(-36) \\[5pt] &=& -\dfrac{5}{9}\times(-36)+\dfrac{1}{2}\times(-36) \\[5pt] &=& 20-18 \\[5pt] &=& 2 \\[5pt] \end{eqnarray}となります。これも、カッコ内を計算して $-\dfrac{1}{18}\times(-36)$ と求めても構いません。

おわりに

ここでは、正の数や負の数の計算での、分配法則について見てきました。とくに分数の計算では計算が簡単になることもあるので、工夫できるときは工夫して計算しましょう。