【基本】反比例を表す式
ここでは、反比例の関係を表す式について見ていきます。
反比例を表す式
【基本】比例を表す式では、比例について見ました。小学校では、比例を学んだときに反比例についても学びました。ここでは、反比例について見ていきます。
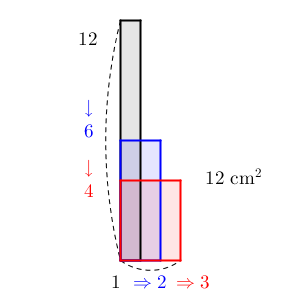
面積が $12\mathrm{cm}^2$ の長方形があるとします。面積を変えずに、縦と横の長さを変えたときの関係を考えてみましょう。
横の長さを、1cm、2cm、3cmと変えるとします。対応する縦の長さは、割り算をすれば求められますね。順番に、12cm、6cm、4cmとなります。横の長さを2倍、3倍、とすると、それにともなって、縦の長さは $\dfrac{1}{2}$ 倍、 $\dfrac{1}{3}$ 倍、となります。
このように、ある量(x で表すとします)が、2倍、3倍、4倍、…となるにともなって、別の量(y で表すとします)が、 $\dfrac{1}{2}$ 倍、 $\dfrac{1}{3}$ 倍、 $\dfrac{1}{4}$ 倍、…と変化していくとき、 $y$ は $x$ に反比例する、と小学校では習っていたと思います。
$y$ が $x$ に反比例するとき、\[ xy \]の値は一定になります。 $x$ が2倍、3倍、4倍、…となるにともなって、 $y$ が、 $\dfrac{1}{2}$ 倍、 $\dfrac{1}{3}$ 倍、 $\dfrac{1}{4}$ 倍、…となっていくので、2つを掛けると打ち消し合うからです。そのため、 $xy$ の値は変わりません。この値のことを、比例定数(proportionality constant) といいます。比例定数を $a$ で表すことにすると、\[ y=\dfrac{a}{x} \]というように、 $y$ を $x$ の式で表すことができます。
数学の世界では、比例のときと同様に、反比例も式を用いて次のように定義します。
反比例のときでも、反比例定数とは言わず、比例定数と呼ぶことに注意しましょう。
横が $x$ cm、縦が $y$ cmで、面積が $12\mathrm{cm}^2$ の長方形であれば、\[ y=\dfrac{12}{x} \]と表すことができます。なので、 $y$ は $x$ に反比例することがわかります。なお、比例定数は $12$ です。
反比例の性質
【基本】比例の性質でも見ましたが、小学校のときとは違い、負の数を学んだので、今後は $x$ に負の数を代入することもできます。反比例の式 $y=\dfrac{12}{x}$ の $x$ にいくつか値を入れてみると、 $y$ の値とは次のように対応します。
| $x$ | $y$ |
|---|---|
| -3 | -4 |
| -2 | -6 |
| -1 | -12 |
| 0 | / |
| 1 | 12 |
| 2 | 6 |
| 3 | 4 |
なお、 $0$ で割ることはできないので $x=0$ のときは考えません。上のように、負の値も考える点が、小学校のときとことなります。また、今後は、比例定数が負となっていることもあります。
反比例の性質として、 $x$ が2倍、3倍、…となるにともなって、 $y$ が、 $\dfrac{1}{2}$ 倍、 $\dfrac{1}{3}$ 倍、…となっていくことは、上のような値の対応表を書くことでも確かめられますし、反比例の式 $y=\dfrac{a}{x}$ を見てもわかるでしょう。また、この式を $xy=a$ と変形すれば、積が一定になることもわかります。この性質も大切です。
例題
(1) 分速 $x$ mで進むとき、1000mの距離を進むのにかかる時間 $y$ 分
(2) 12cmのろうそくが、1分間に $x$ cm短くなっていくとき、3分後に残っている長さ $y$ cm
(1)は、距離を速さで割れば時間が得られるので、\[ y=\dfrac{1000}{x} \]となります。 $y=\dfrac{a}{x}$ で $a=1000$ とすればいいので、反比例する、と言えます。
(2)は、3分後には $3x$ cm短くなっているので、\[ y=12-3x \]となります。 $y=\dfrac{a}{x}$ の $a$ に何を代入しても $12-3x$ にはならないので、反比例するとはいえません。
どちらも、 $x$ が増えるにつれて $y$ は減っていきますが、それと反比例するかどうかは別問題です。反比例の式で表せるか、もしくは、片方を2倍、3倍、…したときに、もう片方が $\dfrac{1}{2}$ 倍、 $\dfrac{1}{3}$ 倍、…となるか、を確認しないといけません。
おわりに
ここでは、反比例を表す式や、反比例の性質を見てきました。反比例は $y=\dfrac{a}{x}$ という式で表すことができます。
また、比例は割ったもの $\dfrac{y}{x}$ が一定、反比例は掛けたもの $xy$ が一定、という性質があります。似ていますが、間違えないようにしましょう。





