【標準】反比例のグラフ
ここでは、反比例のグラフに関連する問題を見ていきます。
反比例のグラフと点に関する問題
$\mathrm{A}(3,6)$ $\mathrm{B}(2,36)$ $\mathrm{C}(-1,17)$
$\mathrm{D}(0,0)$ $\mathrm{E}\left(-12, \dfrac{3}{2}\right)$ $\mathrm{F}\left(\dfrac{3}{4} ,24\right)$
【基本】反比例のグラフで見たように、反比例のグラフは、反比例の式を満たす $(x,y)$ に対応する点をとってつなげたものでした。なので、反比例のグラフの上にある点は、反比例の式を満たすことになります。つまり、この問題であれば、例えば $x=1$, $y=18$ は $y=\dfrac{18}{x}$ を満たすので、点 $(1,18)$ はこのグラフ上にあると判断できる、という具合です。
このことから、順番に代入して、 $y=\dfrac{18}{x}$ を満たすかどうかを確認していけばいいです。 A は、 $x=3$ とすると、 $y=\dfrac{18}{3}=6$ なので、グラフ上にあることがわかります。 $x=2$ とすると、 $y=\dfrac{18}{2}=9$ なので、 B は、グラフ上にはないことがわかります。
C は、 $x=-1$ のときに $y=\dfrac{18}{-1}=-18$ なので、グラフ上にはないことがわかります。また、 $0$ で割ることはできないので、 $x=0$ となることはありません。そのため、 D はグラフ上にはありません。
E は、 $x=-12$ のときに $y=\dfrac{18}{-12}=-\dfrac{3}{2}$ です。 E の $y$ 座標にはマイナスがついていないので、ダメです。グラフ上にはありません。
F は、 $x=\dfrac{3}{4}$ のときを考えるのですが、 $y=\dfrac{18}{x}$ にどのように代入するか難しいですね。分数の中に分数が出てくるのは、今までなかったかもしれません。ただ、 $\dfrac{18}{x}$ は、 $18\div x$ のことだったので、こう変形してから代入すると計算できますね。\[ y=18\div \frac{3}{4}=18\times \frac{4}{3}=24 \]となり、 F はグラフ上にあることがわかります。
以上から、 $y=\dfrac{18}{x}$ のグラフ上にあるのは、点 A と点 F であることがわかります。
反比例のグラフをかく問題
(1) $y=\dfrac{6}{x}$ (2) $y=-\dfrac{8}{x}$
通る点をいくつか選んで、なめらかにつないでいきます。 (1)であれば、 $(1,6)$, $(2,3)$, $(3,2)$ や $(-6, -1)$, $(-3,-2)$ といった点をとってつなぎます。(2)も同様に、通る点をいくつか調べます。 $(1,-8)$, $(2,-4)$, $(4,-2)$ や $(-8, 1)$, $(-4,2)$, $(-2,4)$ などの点をとって、つなぎます。
グラフは次のようになります。

グラフが軸と交わることがないように注意してかきましょう。
反比例のグラフから式を求める問題
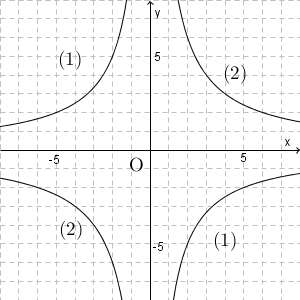
先ほどとは逆に、通っている点から考えていきます。反比例のグラフを求めるには、比例定数がわかればいいですね。 $y=\dfrac{a}{x}$ の $a$ の部分です。これは、 $x$ 座標と $y$ 座標の値を掛ければ求められます。
$x$ 座標も $y$ 座標も、どちらも整数になっている点を探しましょう。(1)であれば、 $(2,-5)$ などが見つかります。これより、比例定数は、\[ 2\times(-5)=-10 \]とわかるので、反比例の式は $y=-\dfrac{10}{x}$ であることがわかります。
(2)は、 $(3,4)$ などが見つかります。これより、比例定数は $3\times 4=12$ とわかるので、反比例の式は $y=\dfrac{12}{x}$ となることがわかります。
おわりに
ここでは、反比例のグラフに関連する問題を見てきました。 $x$ 座標も $y$ 座標も、どちらも整数になっている点を利用して、グラフをかいたり、グラフから式を求めたりしましょう。





