【基本】二次関数のグラフとx軸との共有点
ここでは、二次関数のグラフと x 軸との共有点の個数について見ていきます。
二次関数のグラフとx軸との交点
二次関数 $y=ax^2+bx+c$ のグラフをかく場合、軸とどう交わるかというのも重要な情報です。y 軸との交点が $(0,c)$ であることはわかりますが、x 軸との共有点はどうなるでしょうか。まずは、x 軸と2点で交わっているときの、交点について考えてみましょう。
この放物線上の点は $(x,ax^2+bx+c)$ と書けます。また、x 軸上の点の y 座標は0なので、 $(x,0)$ と書けます。 y 座標同士を比較すると、交点の x 座標は次の二次方程式\[ ax^2+bx+c=0 \]の解になることがわかります。
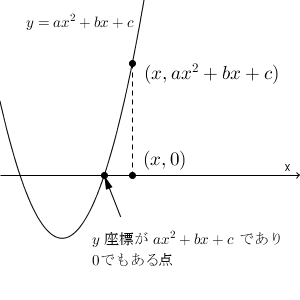
つまり、この二次方程式の解を $x=s,t$ とすると、グラフと x 軸との交点は $(s,0),(t,0)$ となる、ということですね。
二次関数のグラフとx軸との共有点の数
二次関数のグラフが x 軸と2点で交わっているときを考えましたが、グラフが x 軸と交わらないケースもあります。この違いはどこから来るのでしょう。
上で見たように、「二次関数のグラフと x 軸との共有点」と「二次方程式の実数解」が対応していましたね。同様に考えれば、共有点が1点だけの場合や共有点が無い場合でも、同じように対応することが分かります。つまり、共有点の数と実数解の個数が対応する、ということです。
二次方程式の解の個数を考えるために、判別式というものを使いました(参考:【基本】二次方程式の解の個数と判別式)。これらを組み合わせて、判別式の符号、二次方程式の解の個数、二次関数のグラフと x 軸との共有点の個数、それぞれの対応を表にすると、次のようになります。
| 判別式 $D$ | $D\gt 0$ | $D=0$ | $D\lt 0$ |
|---|---|---|---|
| 二次方程式 $ax^2+bx+c=0$ の解の個数 | 異なる 2つの 実数解 | 1つの 実数解 (重解) | 実数解なし |
| 二次関数 $y=ax^2+bx+c$ のグラフとx軸との 共有点の個数 | 2個 | 1個 | なし |
接点
二次関数のグラフ(定義域が実数全体のもの)とx軸との共有点が1点だけの場合、「二次関数のグラフはx軸に接する」といいます。そして、この共有点のことを接点(point of tangency)といいます。
今までの話からもわかると思いますが、接点のx座標は、二次方程式の重解に対応しています。
判別式と二次関数のグラフとの関係
上では、「二次関数と二次方程式」「二次方程式と判別式」の2つの関連性を組み合わせて考えましたが、判別式と「二次関数のグラフとx軸との共有点の数」との関係を直接見てみましょう。
二次関数 $y=ax^2+bx+c$ のグラフとx軸との共有点を考えるために、まずは頂点の座標を考えてみます。次のように平方完成をすればわかりますね。
\begin{eqnarray}
y
&=&
ax^2+bx+c \\[5pt]
&=&
a\left(x^2+\frac{b}{a}x\right)+c \\[5pt]
&=&
a\left(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}\right) -\frac{b^2}{4a}+c \\[5pt]
&=&
a\left(x+\frac{b}{2a}\right)^2 -\frac{b^2-4ac}{4a} \\[5pt]
\end{eqnarray}このことから、頂点の y 座標は $\displaystyle -\frac{b^2-4ac}{4a}$ であることが分かります。特に、分子にあるのは、判別式 $D=b^2-4ac$ と同じであることに注意しましょう。
$a\gt 0$ の場合、下に凸の放物線になります。このとき、 $D=b^2-4ac$ が正であれば、頂点のy座標は、分母・分子が正で前にマイナスがついているので、y座標がマイナスになることが分かります。下に凸で頂点のy座標がマイナスなので、必ず x 軸と2点で交わることが分かります。

$D=0$ なら、頂点はx軸上に来ることがわかります。共有点が1点だけの場合、この共有点のことを接点というんでしたね。

また $D\lt 0$ なら頂点のy 座標はプラスになり、x軸と共有点を持たないことが分かります。
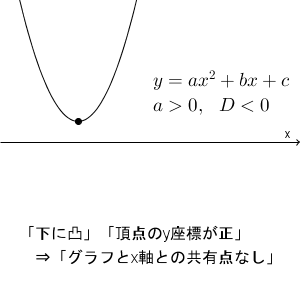
このように考えれば、二次方程式を間に介さなくても、判別式と二次関数のグラフとの関係を直接見ることができます。a が負のときも、「二次関数のグラフとx軸との共有点の数」と判別式の符号とが対応していることは、同じように考えることができます。
おわりに
ここでは、二次関数のグラフと x 軸との共有点について見てきました。判別式を使えば共有点の数がわかり、グラフと x 軸との位置関係もわかります。
ここの内容は、二次不等式を解く際にも必要になってくるので、よく理解しておきましょう。





