【基本】2曲線間の面積と積分の復習

🕒 2018/12/19 🔄 2023/05/01

ここでは、2曲線で囲まれた部分の面積を、積分を使って求める方法について見ていきます。

📘 目次

2曲線間の面積と積分の復習

【基本】2曲線間の面積と積分でも見ましたが、 $y=f(x)$, $y=g(x)$ で囲まれた部分の面積も、定積分を使って求めることができます。

【基本】x軸とで囲まれた部分の面積と積分でも見ましたが、 $a\leqq x\leqq b$ の範囲で $f(x)\geqq 0$ のとき、 $y=f(x)$, $x$ 軸, $x=a$, $x=b$ で囲まれた部分の面積は\[ \int_a^b f(x)dx \]で求めることができます。

これを利用すれば、 $f(x)\geqq g(x)$ のとき、 $y=f(x)$, $y=g(x)$, $x=a$, $x=b$ で囲まれた部分も定積分で表すことができます。

上の図の青い部分は「 $x=a$, $x=b$, $y=f(x)$, x 軸で囲まれた部分」から「 $x=a$, $x=b$, $y=g(x)$, x 軸で囲まれた部分」を引けばいいですね。

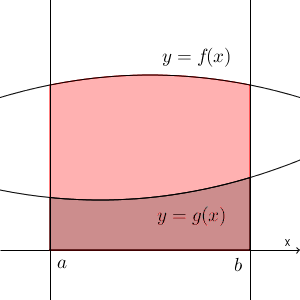
よって、\[ \int_a^b \{ f(x)-g(x) \}dx \]を計算すれば、2曲線の間にある部分の面積が求められます。

もし、 $y=f(x)$, $y=g(x)$ が $x$ 軸より下になってしまう範囲があれば、両方に適当に正の数を足せばいいです。図でいうと、2つの曲線を、同じように上に移動させる、ということですね。 $y=f(x)+k$, $y=g(x)+k$ として考えればいいのですが、計算すると、結局 $k$ が消えて、上の式に戻ります。

2つの曲線で囲まれた部分の面積

連続な関数 $f(x),g(x)$ は、 $a\leqq x \leqq b$ で、 $f(x)\geqq g(x)$ であるとする。このとき、 $x=a$, $x=b$, $y=f(x)$, $y=g(x)$ で囲まれた部分の面積 S について、次が成り立つ。\[ S=\int_a^b \{ f(x)-g(x) \} dx \]

こちらを基準に考えれば、「 $x=a$, $x=b$, $y=f(x)$, x 軸で囲まれた部分」というのは、 $g(x)=0$ としたときだととらえることもできます。

積分を使って面積を求める

例題

$0\leqq x \leqq 2\pi$ の区間で、 $y=\sin x$ と $y=\cos x$ で囲まれた部分の面積を求めなさい。

$y=\sin x$, $y=\cos x$ のグラフをかくと、次のようになります。

囲まれた部分が真ん中の方にありますね。この部分の面積は、定積分で求めることができるのですが、まずは、積分区間がわからないとダメですね。まずは交点を求めましょう。

\[ \sin x=\cos x \]とします。相互関係 $\sin^2 x+\cos^2 x=1$ に代入して\[ \sin x=\pm\frac{1}{\sqrt{2} } \]となることがわかります。これをもとに、 $0\leqq x\leqq 2\pi$ の範囲で $\sin x=\cos x$ を満たすものは、\[ x=\frac{1}{4}\pi,\frac{5}{4}\pi \]であることがわかります。

また、 $\dfrac{1}{4}\pi\leqq x\leqq \dfrac{5}{4}\pi$ の範囲では、 $\sin x\geqq \cos x$ なので、囲まれた部分の面積は
\begin{eqnarray} & & \int_{\frac{1}{4}\pi}^{\frac{5}{4}\pi} (\sin x-\cos x) dx \\[5pt] &=& \Big[ -\cos x-\sin x \Big]_{\frac{1}{4}\pi}^{\frac{5}{4}\pi} \\[5pt] &=& \left(\frac{1}{\sqrt{2} }+\frac{1}{\sqrt{2} }\right)-\left(-\frac{1}{\sqrt{2} }-\frac{1}{\sqrt{2} }\right) \\[5pt] &=& 2\sqrt{2} \end{eqnarray}となることがわかります。

はじめの頃は、こんな部分の面積が求められることを不思議に感じる人も多いでしょう。今まで見てきた、微分・積分の計算が、こうした面積の話に発展していくのはおもしろいですね。これから、他にもいろいろな面積や体積を求めていくことになります。