【基本】角と三角形

ここでは、図形を考えていく上で基本となる、角や三角形・四角形に関する用語を見ていきます。これらも、【基本】点と直線と同様に、すでに見たことがあるものが多いでしょう。

角

下の図のように、2つの半直線OA, OB によってできる図形を、角(angle) といいます。ちなみに、半直線とは、【基本】点と直線で見たように、片方の点から出発してもう片方の点のほうへ伸びていく線のことを言います。

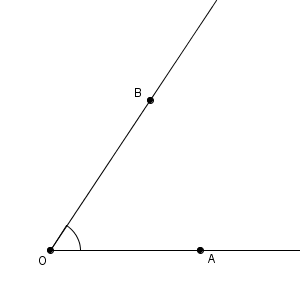
角に対して、2つの半直線の共有点を、角の頂点といいます。角は、 $\angle$ という記号を用いて、 $\angle \mathrm{ O }$ と表します。また、2つの半直線OA, OB から作られる角であることをはっきりと示すために、 $\angle \mathrm{ AOB }$ とも書きます。図では、上のように、該当する箇所を小さい曲線を使って表します。

角の大きさを、角度といいます。

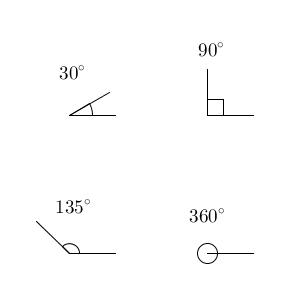
一周を $360^{\circ}$ とし、一周との比で角度を表します。単位は「°」を使い、度と読みます。例えば、 $\angle \mathrm{ AOB }=30^{\circ}$ というと、 $\angle \mathrm{ AOB }$ の大きさは、一周の $\dfrac{30}{360}=\dfrac{1}{12}$ だ、ということです。

2つの角度が等しいときは、「＝」を使って、\[ \mathrm{ \angle ABC = \angle DEF } \]というように表します。

直角と垂直

$90^{\circ}$ のことを、直角(right angle) といいます。

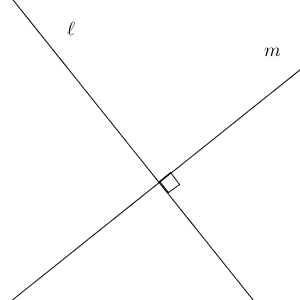
上の図では、2つの直線が交わって4つの角ができていますが、どの角も同じ角です。バランスのとれた状態になっていますね。こうした特徴的な角なので、直角は特別扱いをします。

普通、図の中で角度を表すときには、小さな丸い曲線を使いますが、直角の場合は、上の図のように、"┐" という記号を使って表します。記号も特別に用意されています。

2つの直線が交わり、そのときにできる角が直角のとき、2つの直線は垂直(perpendicular) である、といいます。2つの直線 $\ell, m$ が垂直であることを、 $\perp$ という記号を使って、\[ \ell \perp m \]と書きます。

また、ある直線に対して、この直線に垂直な直線のことを垂線(perpendicular line) といいます。

線分の場合も、垂直や垂線を同じように定義します。

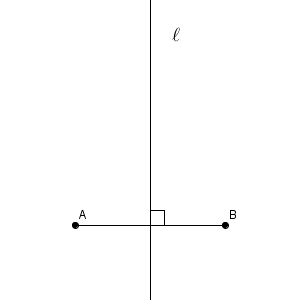
上の図では、線分AB と直線 $\ell$ とが交わってできる角が直角なので、 $\mathrm{ AB } \perp \ell$ と表します。直線 $\ell$ は、線分AB の垂線です。

三角形

一直線上にない3点があったときに、この3点を線分で結んでできる図形を、三角形(triangle) といいます。

この3点のことを頂点といい、3つの線分を辺といいます。三角形を呼ぶときは、3つの頂点の名前を使って、三角形ABC と書いたり、記号を用いて $\triangle \mathrm{ ABC }$ と書いたりします。

三角形のことを、英語では、 triangle といいます。angle は「角」のことです。tri は、トリプルやトリオなどに共通する、「3」を表すものです。つまり、「3つの角」ということで、三角形に対応していることがわかります。

特徴のある三角形には、特別な名前がついています。2つの辺が等しい三角形を二等辺三角形、直角を含む三角形を直角三角形、直角三角形でも二等辺三角形でもある三角形のことを直角二等辺三角形、3辺が等しい三角形を正三角形といいます。

多角形

三角形は、3つの頂点と3つの辺をもつ図形でしたが、4つの頂点と4つの辺をもつ図形は四角形といい、5つの頂点と5つの辺をもつ図形は五角形といいます。以降、 $n$ 個の頂点と $n$ 本の辺をもつ図形は、 $n$ 角形といいます。

また、 $n$ 角形のすべての辺の長さが等しく、すべての角の大きさも等しいとき、正 $n$ 角形といいます。 $n=4$ のときだけ、正四角形ではなく正方形という特別な呼び方をします。

三角形、四角形、五角形、…をまとめて、多角形といいます。正三角形、正方形、正五角形、…をまとめて、正多角形といいます。

おわりに

ここでは、角や三角形、四角形などに関する用語を見てきました。三角形と四角形については、今後さらに詳しく見ていくことになります。