東京大学 理系 2022年度 第5問 解説
問題編
問題
座標空間内の点 $\mathrm{ A }(0,0,2)$ と点 $\mathrm{ B }(1,0,1)$ を結ぶ線分 AB を $z$ 軸のまわりに1回転させて得られる曲面を $S$ とする。 $S$ 上の点 P と $xy$ 平面上の点 Q が $\mathrm{ PQ }=2$ を満たしながら動くとき、線分 PQ の中点 M が通過しうる範囲を $K$ とする。 $K$ の体積を求めよ。
考え方
動くものが多いので、何かを固定したり、ある平面で切ったりして、状況をシンプルにしてから考えましょう。
体積を積分で表した後も計算は楽ではなく、解ききるのは難しいです。何を変数にするかによっても、難易度は変わってくるでしょう。
解答編
問題
座標空間内の点 $\mathrm{ A }(0,0,2)$ と点 $\mathrm{ B }(1,0,1)$ を結ぶ線分 AB を $z$ 軸のまわりに1回転させて得られる曲面を $S$ とする。 $S$ 上の点 P と $xy$ 平面上の点 Q が $\mathrm{ PQ }=2$ を満たしながら動くとき、線分 PQ の中点 M が通過しうる範囲を $K$ とする。 $K$ の体積を求めよ。
解答
線分 AB は平面 $y=0$ 上にあり、 $z=-x+2$ $(0\leqq x\leqq 1)$ で表すことができる。
まずは P が線分 AB 上にあるときを考える。 P の座標を $(p,0,-p+2)$ とおく $(0\leqq p \leqq 1)$。
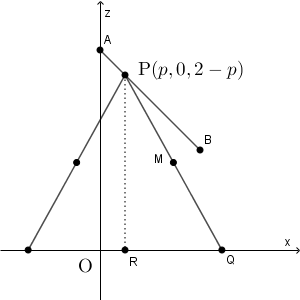
上の図は、さらに、平面 $y=0$ で切った断面図である。点 P から $x$ 軸に下した垂線の足を R とする。 $\mathrm{ PQ }=2$ を満たしながら動くとき、\[ \mathrm{ RQ }=\sqrt{2^2-(2-p)^2} \]である。よって、 Q は、 $xy$ 平面上で、点 $(p,0,0)$ を中心とした半径 $\sqrt{4-(2-p)^2}$ の円周上を動く。
よって M は、平面 $z=\dfrac{2-p}{2}$ 上で、点 $\left(p,0,\dfrac{2-p}{2}\right)$ を中心とした、半径 $\dfrac{\sqrt{4-(2-p)^2} }{2}$ の円周上を動く。
ここで、 $z_0=\dfrac{2-p}{2}$ と置きなおすと、 $0\leqq p\leqq 1$ より $\dfrac{1}{2}\leqq z_0\leqq 1$ であり、 $p=2-2z_0$ である。また、
\begin{eqnarray}
\dfrac{\sqrt{4-(2-p)^2} }{2}
&=&
\dfrac{\sqrt{4-(2z_0)^2} }{2} \\[5pt]
&=&
\sqrt{1-z_0^2} \\[5pt]
\end{eqnarray}となる。つまり、言い換えると、 M は平面 $z=z_0$ 上で、点 $(2-2z_0,0,z_0)$ を中心とした半径 $\sqrt{1-z_0^2}$ の円周上を動くことがわかる。
これより、 $K$ を平面 $z=z_0$ で切ったときの断面は、上で求めた円周を $z$ 軸を中心に1回転してできる図形となる。
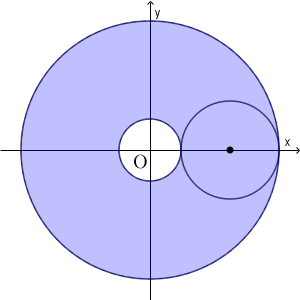
$2-2z_0-\sqrt{1-z_0^2}$ が正の場合は、上のように、半径 $2-2z_0+\sqrt{1-z_0^2}$ の円から半径 $2-2z_0-\sqrt{1-z_0^2}$ の円をくりぬいた部分となる。
一方、 $2-2z_0-\sqrt{1-z_0^2}$ が負の場合は、次のようになる。
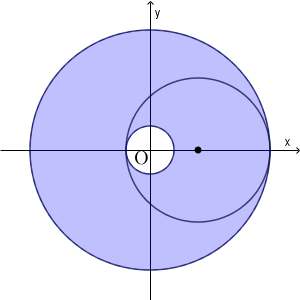
半径 $2-2z_0+\sqrt{1-z_0^2}$ の円から半径 $\sqrt{1-z_0^2}-2-2z_0$ の円をくりぬいた部分となる(内側の円と外側の円の両方に接しながら、半径 $\sqrt{1-z_0^2}$ の円が動く)。
このことから、断面の面積は
\begin{eqnarray}
& &
\pi (2-2z_0+\sqrt{1-z_0^2})^2 -\pi (2-2z_0-\sqrt{1-z_0^2})^2 \\[5pt]
&=&
\pi \cdot 4(2-2z_0)\sqrt{1-z_0^2} \\[5pt]
&=&
8\pi (1-z_0)\sqrt{1-z_0^2} \\[5pt]
\end{eqnarray}となる。このことから、 $K$ の体積は
\begin{eqnarray}
& &
\int_{1/2}^1 8\pi (1-z)\sqrt{1-z^2} dz
\end{eqnarray}とかける。 $z=\sin t$ とすると、この体積は
\begin{eqnarray}
& &
8\pi \int_{\pi/6}^{\pi/2} (1-\sin t) \cos t \cdot \cos t dt \\[5pt]
&=&
8\pi \int_{\pi/6}^{\pi/2} (\cos^2 t-\sin t\cos^2 t) dt\\[5pt]
&=&
8\pi \int_{\pi/6}^{\pi/2} \left(\frac{\cos 2t+1}{2}-\sin t\cos^2 t\right) dt \\[5pt]
&=&
8\pi \left[ \frac{\sin 2t}{4} +\frac{t}{2}+\frac{1}{3}\cos^3 t \right]_{\pi/6}^{\pi/2} \\[5pt]
&=&
8\pi \left( \frac{-\frac{\sqrt{3} }{2} }{4} +\frac{\frac{\pi}{2}-\frac{\pi}{6} }{2}-\frac{1}{3} \cdot\frac{3\sqrt{3} }{8} \right) \\[5pt]
&=&
8\pi \left( -\frac{\sqrt{3} }{8} +\frac{\pi}{6}-\frac{3\sqrt{3} }{8} \right) \\[5pt]
&=&
\frac{4}{3}\pi^2 -2\sqrt{3}\pi
\end{eqnarray}となる。(答)





