東京大学 理系 2022年度 第4問 解説
問題編
問題
座標平面上の曲線\[ C:\ y=x^3-x \]を考える。
(1) 座標平面上のすべての点 P が次の条件(i) を満たすことを示せ。
(i) 点 P を通る直線 $\ell$ で、曲線 $C$ と相異なる3点で交わるものが存在する。
(2) 次の条件(ii)を満たす点 P のとりうる範囲を座標平面上に図示せよ。
(ii) 点 P を通る直線 $\ell$ で、曲線 $C$ と相異なる3点で交わり、かつ、直線 $\ell$ と曲線 $C$ で囲まれた2つの部分の面積が等しくなるものが存在する。
考え方
(1)の「異なる3点で交わる」はよく出てくる条件です。点の場所も直線の傾きも決まっていないため抽象的ですが、似た問題でどういうことをやっていたか思い出しましょう。
(2)は、直線の方程式を使って面積を計算して条件をしぼっていくやり方でもできますが、対称性を利用して計算量を減らして解いていくこともできます。
解答編
問題
座標平面上の曲線\[ C:\ y=x^3-x \]を考える。
(1) 座標平面上のすべての点 P が次の条件(i) を満たすことを示せ。
(i) 点 P を通る直線 $\ell$ で、曲線 $C$ と相異なる3点で交わるものが存在する。
解答
(1)
点 P の座標を $(a,b)$ とする。
$\ell$ の傾きを $m$ とする。また、以下では $m$ は正の実数とする。このとき、直線 $\ell$ の方程式は\[ y=m(x-a)+b \]である。これと曲線 $C$ との交点の $x$ 座標は
\begin{eqnarray}
x^3-x &=& m(x-a)+b \\[5pt]
x^3-(m+1)x+am-b &=& 0 \\[5pt]
\end{eqnarray}の解と一致する。最後の式の左辺を $f(x)$ とおく。
$f'(x)=3x^2-(m+1)$ なので、 $f'(x)=0$ となるのは $x=\pm\sqrt{\dfrac{m+1}{3} }$ のときである。よって、増減表は次のようになる。
\begin{array}{c|ccccc}
x & \cdots & -\sqrt{\tfrac{m+1}{3} } & \cdots & \sqrt{\tfrac{m+1}{3} } & \cdots \\
\hline
f'(x) & + & 0 & - & 0 & + \\
\hline
f(x) & \nearrow & & \searrow & & \nearrow
\end{array}ここで、
\begin{eqnarray}
& &
f\left(\sqrt{\dfrac{m+1}{3} }\right) \\[5pt]
&=&
\dfrac{m+1}{3}\sqrt{\dfrac{m+1}{3} }-(m+1)\sqrt{\dfrac{m+1}{3} }+am-b \\[5pt]
&=&
-\dfrac{2(m+1)}{3}\sqrt{\dfrac{m+1}{3} }+a(m+1)-a-b \\[5pt]
&=&
(m+1)\left(a-\frac{2}{3}\sqrt{\dfrac{m+1}{3} }\right)-a-b \\[5pt]
\end{eqnarray}であり
\begin{eqnarray}
& &
f\left(-\sqrt{\dfrac{m+1}{3} }\right) \\[5pt]
&=&
-\dfrac{m+1}{3}\sqrt{\dfrac{m+1}{3} }+(m+1)\sqrt{\dfrac{m+1}{3} }+am-b \\[5pt]
&=&
\dfrac{2(m+1)}{3}\sqrt{\dfrac{m+1}{3} }+a(m+1)-a-b \\[5pt]
&=&
(m+1)\left(a+\frac{2}{3}\sqrt{\dfrac{m+1}{3} }\right)-a-b \\[5pt]
\end{eqnarray}となる。 $m\to\infty$ のとき $f\left(\sqrt{\dfrac{m+1}{3} }\right)\to -\infty$ であり、 $f\left(-\sqrt{\dfrac{m+1}{3} }\right)\to +\infty$ であるから、 $m$ を十分大きくとれば、極大値が正で極小値が負になるようにできる。また、 $x\to\infty$ のとき $f(-x)\to-\infty$ かつ $f(x)\to\infty$ となることから、上のようにとった $m$ について、 $y=f(x)$ は $x$ 軸と異なる3点で交わることがわかる。
以上から、条件(i)を満たすことが示せた。
解答編 つづき
問題
(2) 次の条件(ii)を満たす点 P のとりうる範囲を座標平面上に図示せよ。
(ii) 点 P を通る直線 $\ell$ で、曲線 $C$ と相異なる3点で交わり、かつ、直線 $\ell$ と曲線 $C$ で囲まれた2つの部分の面積が等しくなるものが存在する。
解答
(2)
直線 $\ell$ が曲線 $C$ と相異なる3点で交わっており、かつ、直線 $\ell$ と曲線 $C$ で囲まれた2つの部分の面積が等しいとする。
曲線 $C$ と直線 $\ell$ で囲まれた2つの部分のうち、左側の部分の面積を $L_1$, 右側の部分の面積を $R_1$ と書くことにする。
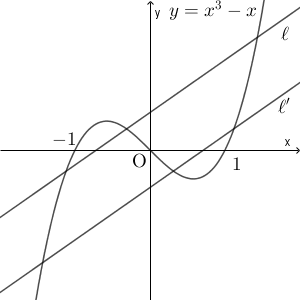
曲線 $C$ は原点について点対称である。直線 $\ell$ を原点について点対称に移動した直線を $\ell'$ とすると、この直線も曲線 $C$ と相異なる2点で交わるため、囲まれた2つの部分のうち、左側の部分の面積を $L_2$, 右側の部分の面積を $R_2$ と書くことにする。
仮定より、 $L_1=R_1$ である。また、点対称移動により図形の面積は変わらないので、 $R_1=L_2$ が成り立つ。よって、 $L_1=L_2$ となる。
直線 $\ell$, $\ell'$ は平行であることから、一致していなければ面積は等しくならない。よって、2直線は一致し、直線 $\ell$ は原点について点対称であることがわかる。つまり、条件(ii)にある直線 $\ell$ は、原点を通ることがわかる。
$p\ne 0$ とし、直線 $\ell$ が $(0,0)$, $(p,p^3-p)$ を通るとすると、 $(-p.-p^3+p)$ も通る。このとき、曲線 $C$ と直線 $\ell$ はこれらの相異なる3点で交わることがわかる。また、対称性より、2つの部分の面積が等しいこともわかる。
以上から求める範囲は、原点と原点以外の曲線 $C$ 上の点を結んだ直線上にある点すべて、となる。この直線の傾きは
\begin{eqnarray}
\frac{p^3-p-0}{p-0}=p^2-1
\end{eqnarray}となるので、 $-1$ より大きいすべての値をとりうる。
このことから、求める範囲は、下の図の色のついた部分。ただし、境界線上の点は原点のみ含む。
(答)






