東京大学 理系 2022年度 第3問 解説

問題編

問題

　O を原点とする座標平面上で考える。座標平面上の2点 $\mathrm{ S }(x_1,y_1)$, $\mathrm{ T }(x_2,y_2)$ に対し、点 $\mathrm{ S }$ が点 $\mathrm{ T }$ から十分離れているとは、

　$|x_1-x_2|\geqq 1$ または $|y_1-y_2|\geqq 1$

が成り立つことと定義する。

　不等式\[ 0\leqq x\leqq 3,\ 0\leqq y\leqq 3 \]が表す正方形の領域を $D$ とし、その2つの頂点 $\mathrm{ A }(3,0)$, $\mathrm{ B }(3,3)$ を考える。さらに、次の条件(i), (ii)をともに満たす点 $\mathrm{ P }$ をとる。

　(i) 点 $\mathrm{ P }$ は領域 $D$ の点であり、かつ、放物線 $y=x^2$ 上にある。
　(ii) 点 $\mathrm{ P }$ は、3点 $\mathrm{ O, A, B }$ のいずれからも十分離れている。

点 $\mathrm{ P }$ の $x$ 座標を $a$ とする。

(1) $a$ のとりうる値の範囲を求めよ。

(2) 次の条件(iii), (iv)をともに満たす点 $\mathrm{ Q }$ が存在しうる範囲の面積 $f(a)$ を求めよ。

　(iii) 点 $\mathrm{ Q }$ は領域 $D$ の点である。
　(iv) 点 $\mathrm{ Q }$ は、4点 $\mathrm{ O,A,B,P }$ のいずれからも十分離れている。

(3) $a$ は(1)で求めた範囲を動くとする。(2)の $f(a)$ を最小にする $a$ の値を求めよ。

考え方

「十分離れている」は、この問題特有の設定ですが、内容自体は難しくないです。「十分離れている」をメインに考える方法も「十分離れていない」をメインに考える方法もあります。自分の考えやすい方を選択しましょう。

(2)はいろいろ図をかいて見て、どういう状況がありうるかを考えます。(3)は何がやりたいのかよくわからず、本当にこれで答えでいいのかと不安になります。

---

解答編

問題

　O を原点とする座標平面上で考える。座標平面上の2点 $\mathrm{ S }(x_1,y_1)$, $\mathrm{ T }(x_2,y_2)$ に対し、点 $\mathrm{ S }$ が点 $\mathrm{ T }$ から十分離れているとは、

　$|x_1-x_2|\geqq 1$ または $|y_1-y_2|\geqq 1$

が成り立つことと定義する。

　不等式\[ 0\leqq x\leqq 3,\ 0\leqq y\leqq 3 \]が表す正方形の領域を $D$ とし、その2つの頂点 $\mathrm{ A }(3,0)$, $\mathrm{ B }(3,3)$ を考える。さらに、次の条件(i), (ii)をともに満たす点 $\mathrm{ P }$ をとる。

　(i) 点 $\mathrm{ P }$ は領域 $D$ の点であり、かつ、放物線 $y=x^2$ 上にある。
　(ii) 点 $\mathrm{ P }$ は、3点 $\mathrm{ O, A, B }$ のいずれからも十分離れている。

点 $\mathrm{ P }$ の $x$ 座標を $a$ とする。

(1) $a$ のとりうる値の範囲を求めよ。

解答

(1)
まず、条件(i)を満たす $a$ の範囲は $0\leqq a \leqq \sqrt{3}$ である。

（上の図の色のついた部分は、「十分離れていない」点の範囲。境界線上の点は含まない。）

$0\leqq a\lt 1$ のとき、点 P の $x$ 座標も $y$ 座標も、 $0$ 以上 $1$ 未満なので、点 P は点 O から十分離れてはいない。

一方、 $1\leqq a \leqq \sqrt{3}$ のとき、 $x$ 座標は $1$ 以上なので、P は O から十分離れている。また、 $x$ 座標が $3-1$ 以下なので、 A, B からも十分離れている。

以上から、 $a$ のとりうる値の範囲は $1\leqq a \leqq \sqrt{3}$ である。（答）

解答編　つづき

問題

(2) 次の条件(iii), (iv)をともに満たす点 $\mathrm{ Q }$ が存在しうる範囲の面積 $f(a)$ を求めよ。

　(iii) 点 $\mathrm{ Q }$ は領域 $D$ の点である。
　(iv) 点 $\mathrm{ Q }$ は、4点 $\mathrm{ O,A,B,P }$ のいずれからも十分離れている。

解答

(2)
点 $\mathrm{ X }$ に対し、 $\mathrm{ X }$ から十分離れていない点の集合を $S_{\mathrm{X} }$ と表す。この $S_{\mathrm{X} }$ は、1辺が $2$ の正方形であり、各辺は $x$ 軸か $y$ 軸に平行で、対角線の交点が $\mathrm{ X }$ となっている（ただし、境界線上の点は含まない）。

(iii)を満たすが(iv)を満たさない範囲を考える。これは、 $S_{\mathrm{O} } \cup S_{\mathrm{A} } \cup S_{\mathrm{B} } \cup S_{\mathrm{P} }$ と領域 $D$ との共有部分である。

(ア) $1\leqq a\leqq \sqrt{2}$ のとき

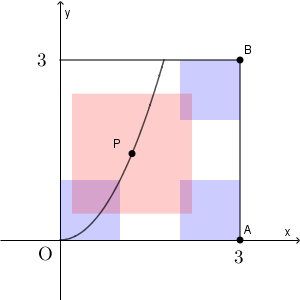
(iii)を満たすが(iv)を満たさない範囲は、上の図の色のついた部分。以下では、4つの正方形の面積の合計 $4+1+1+1=7$ から、重なっている部分の面積を引くことを考える。

$S_{\mathrm{P} }\cap S_{\mathrm{O} }$ の面積は、横が $1-(a-1)=2-a$ で縦が $1-(a^2-1)=2-a^2$ の長方形の面積なので $(2-a)(2-a^2)$ である。

$S_{\mathrm{P} }\cap S_{\mathrm{A} }$ の面積は、横が $(a+1)-2=a-1$ で縦が $2-a^2$ の長方形の面積なので $(a-1)(2-a^2)$ である。

$S_{\mathrm{P} }\cap S_{\mathrm{B} }$ の面積は、横が $a-1$ で縦が $(a^2+1)-2=a^2-1$ の長方形の面積なので $(a-1)(a^2-1)$ である。

よって、(iii)を満たすが(iv)を満たさない範囲の面積は
\begin{eqnarray} & & (4+1+1+1)-(2-a)(2-a^2)\\ & & -(a-1)(2-a^2)-(a-1)(a^2-1) \\[5pt] &=& 7-(2-a)(2-a^2)-(a-1)(2-a^2+a^2-1) \\[5pt] &=& 7-(a^3-2a^2-2a+4)-a+1 \\[5pt] &=& -a^3+2a^2+a+4 \end{eqnarray}となるので、 \begin{eqnarray} f(a) &=& 9-(-a^3+2a^2+a+4) \\[5pt] &=& a^3-2a^2-a+5 \end{eqnarray}となる。

(イ) $\sqrt{2} \lt a\leqq \sqrt{3}$ のとき

このとき、 $S_{\mathrm{P} }\cap S_{\mathrm{O} }$ も $S_{\mathrm{P} }\cap S_{\mathrm{A} }$ も空集合である。以下では、4つの正方形の面積の合計 $4+1+1+1=7$ から、重なっている部分と $D$ からはみ出している部分の面積を引くことを考える。

$S_{\mathrm{P} }\cap S_{\mathrm{B} }\cap D$ の面積は、横が $(a+1)-2=a-1$ で縦が $1$ の長方形の面積なので $a-1$ である。

また、$S_{\mathrm{P} }$ が領域 $D$ からはみ出している部分の面積は、横が $2$ で縦が $(a^2+1)-3=a^2-2$ の長方形の面積なので $2a^2-4$ となる。

よって、(iii)を満たすが(iv)を満たさない範囲の面積は
\begin{eqnarray} 7-(a-1)-(2a^2-4) &=& -2a^2-a+12 \end{eqnarray}となるので、 \begin{eqnarray} f(a) &=& 9-(-2a^2-a+12) \\[5pt] &=& 2a^2+a-3 \end{eqnarray}となる。

(ア)(イ)から、
　$1\leqq a\leqq \sqrt{2}$ のときは $f(a)=a^3-2a^2-a+5$
　$\sqrt{2}\lt a\leqq \sqrt{3}$ のときは $f(a)=2a^2+a-3$
（答）

解答編　つづき

問題

(3) $a$ は(1)で求めた範囲を動くとする。(2)の $f(a)$ を最小にする $a$ の値を求めよ。

解答

(3)
$1\leqq a\leqq \sqrt{2}$ のとき、 $f'(a)=3a^2-4a-1$, $f^{\prime\prime}(a)=6a-4$ であるから、この範囲で $f'(a)$ は狭義単調増加である。 $f'(\sqrt{2})\lt 0$ だから、この区間で $f(a)$ は狭義単調減少。

一方、 $\sqrt{2} \lt a\leqq \sqrt{3}$ のとき、 $f'(a)=4a+1$ なので、この区間で $f(a)$ は狭義単調増加。

よって、 $f(a)$ を最小にする $a$ の値は $\sqrt{2}$ である。（答）