東京大学 理系 2017年度 第6問 解説
問題編
問題
点 O を原点とする座標空間内で、一辺の長さが $1$ の正三角形 OPQ を動かす。また、点 $\mathrm{ A }(1,0,0)$ に対して、 $\angle \mathrm{ AOP }$ を $\theta$ とおく。ただし、 $0^{\circ} \leqq \theta \leqq 180^{\circ}$ とする。
(1) 点 Q が $(0,0,1)$ にあるとき、点 P の x 座標がとりうる値の範囲と、 $\theta$ がとりうる値の範囲を求めよ。
(2) 点 Q が平面 $x=0$ 上を動くとき、辺 OP が通過しうる範囲を K とする。 K の体積を求めよ。
考え方
(1)は2点が固定されているので、 P はある円周上を動くことがわかります。よって、図形から取りうる値の範囲が求められます。
(2)は、まず、どういう立体なのか考えましょう。Q が平面 $x=0$ を動いたとき、(1)をどう使えばいいか考えます。
体積の出し方はいろいろありますが、(1)を使うために、平面 $y=0$ での断面を考えたほうがいいでしょう。
解答編
問題
点 O を原点とする座標空間内で、一辺の長さが $1$ の正三角形 OPQ を動かす。また、点 $\mathrm{ A }(1,0,0)$ に対して、 $\angle \mathrm{ AOP }$ を $\theta$ とおく。ただし、 $0^{\circ} \leqq \theta \leqq 180^{\circ}$ とする。
(1) 点 Q が $(0,0,1)$ にあるとき、点 P の x 座標がとりうる値の範囲と、 $\theta$ がとりうる値の範囲を求めよ。
(2) 点 Q が平面 $x=0$ 上を動くとき、辺 OP が通過しうる範囲を K とする。 K の体積を求めよ。
解答
(1)
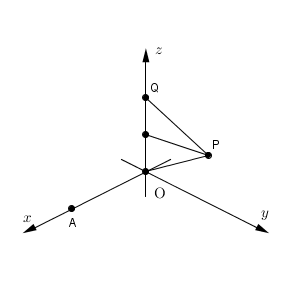
P は、平面 $z=\dfrac{1}{2}$ 上にある、点 $\left(0,0,\dfrac{1}{2}\right)$ を中心とする半径 $\dfrac{\sqrt{3} }{2}$ の円周上を動く。よって、 x 座標がとりうる値は\[ -\frac{\sqrt{3} }{2} \leqq x \leqq \frac{\sqrt{3} }{2} \]である。
三角形 AOP で、 AO と OP の長さは $1$ で固定なので、 $\theta$ が一番小さくなる時と一番大きくなる時は、それぞれ P が A から一番近いときと一番離れているときである。どちらも、 P が平面 $y=0$ にあるときである。
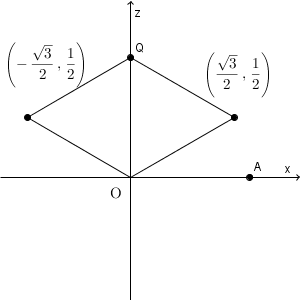
一番近いときは、 $\mathrm{ P }\left(\dfrac{\sqrt{3} }{2},0,\dfrac{1}{2}\right)$ のときで、このとき $\theta =\dfrac{1}{6}\pi$ である。また、一番遠いときは、 $\mathrm{ P }\left(-\dfrac{\sqrt{3} }{2},0,\dfrac{1}{2}\right)$ のときで、このとき $\theta =\dfrac{5}{6}\pi$ である。 $\theta$ は連続的に変化するので、この間の値をすべてとる。
以上から、 x 座標の範囲と $\theta$ の範囲は、それぞれ
\begin{eqnarray}
& & -\frac{\sqrt{3} }{2} \leqq x \leqq \frac{\sqrt{3} }{2} \\[5pt]
& & \frac{1}{6} \pi \leqq \theta \leqq \frac{5}{6}\pi \\[5pt]
\end{eqnarray}となる。
(2)
点 Q を $(0,0,1)$ として P を動かしたときにできる OP の軌跡を、 x 軸に関して回転させたものが K である。
K を 平面 $y=0$ で切ると、 $z\geqq 0$ の部分の断面は、 $\mathrm{ OP }=1$ と(1)より、次の色のついた部分となる。

これを x 軸を中心に回転させたものの体積を求めればよいので、求める体積は
\begin{eqnarray}
& &
2\int_0^{\frac{\sqrt{3} }{2} } \pi (1-x^2)dx -2\times \left(\frac{1}{2}\right)^2\pi\cdot\frac{\sqrt{3} }{2}\cdot\frac{1}{3} \\[5pt]
&=&
2\pi \left[ x-\frac{1}{3}x^3 \right]_0^{\frac{\sqrt{3} }{2} } -\frac{\sqrt{3}\pi}{12} \\[5pt]
&=&
2\pi \left(\frac{\sqrt{3} }{2} -\frac{1}{3} \cdot \frac{3\sqrt{3} }{8}\right) -\frac{\sqrt{3}\pi}{12} \\[5pt]
&=&
2\pi \cdot \frac{3\sqrt{3} }{8} -\frac{\sqrt{3}\pi}{12} \\[5pt]
&=&
\frac{2\sqrt{3}\pi}{3}
\end{eqnarray}となる。
(終)
解説
(1)は図形的に考えていますが、 $\theta$ のとりうる範囲をもう少し厳密に求めるなら、内積などを使いましょう。
(2)は、円錐の側面を x 軸を中心に回転させた図形の体積を求めることになります。平面 $y=0$ での断面を考えるとおうぎ形になるので、この回転体の体積を求めると答えになります。





