東京大学 理系 2017年度 第3問 解説
問題編
問題
複素数平面上の原点以外の点 z に対して、 $w=\dfrac{1}{z}$ とする。
(1) $\alpha$ を $0$ でない複素数とし、点 $\alpha$ と原点 O を結ぶ線分の垂直二等分線を L とする。点 z が直線 L 上を動くとき、点 w の軌跡は円から1点を除いたものになる。この円の中心と半径を求めよ。
(2) $1$ の3乗根のうち、虚部が正であるものを $\beta$ とする。点 $\beta$ と点 $\beta^2$ を結ぶ線分上を点 z が動くときの点 w の軌跡を求め、複素数平面上に図示せよ。
考え方
(1)はほとんど答えが書かれています。垂直二等分線を式で表して考えましょう。実部・虚部と分けるのではなく、複素数の絶対値のまま考えていくほうがいいでしょう。
(2)は(1)から円の一部になることはすぐにわかります。線分の上だけしか移動しないことを言いかえれば、求める軌跡が得られます。
解答編
問題
複素数平面上の原点以外の点 z に対して、 $w=\dfrac{1}{z}$ とする。
(1) $\alpha$ を $0$ でない複素数とし、点 $\alpha$ と原点 O を結ぶ線分の垂直二等分線を L とする。点 z が直線 L 上を動くとき、点 w の軌跡は円から1点を除いたものになる。この円の中心と半径を求めよ。
(2) $1$ の3乗根のうち、虚部が正であるものを $\beta$ とする。点 $\beta$ と点 $\beta^2$ を結ぶ線分上を点 z が動くときの点 w の軌跡を求め、複素数平面上に図示せよ。
解答
(1)
点 z は、点 $\alpha$ と原点を結ぶ線分の垂直二等分線上にあるので
\begin{eqnarray}
|z-0| &=& |z-\alpha|
\end{eqnarray}が成り立つ。 $wz=1$ だから $w\ne 0$ であり、このとき $z=\dfrac{1}{w}$ なので
\begin{eqnarray}
|z| &=& |z-\alpha| \\[5pt]
\left| \frac{1}{w} \right| &=& \left| \frac{1}{w}-\alpha \right| \\[5pt]
1 &=& \left| 1-w\alpha \right| \\[5pt]
\end{eqnarray}となる。ここで、 $\alpha \ne 0$ なので、さらに次のように変形できる。
\begin{eqnarray}
\left| \frac{1}{\alpha} \right| &=& \left| \frac{1}{\alpha}-w \right| \\[5pt]
\left| w-\frac{1}{\alpha} \right| &=& \frac{1}{|\alpha|} \\[5pt]
\end{eqnarray}逆に、この最後の式を満たす $0$ 以外の w に対して、計算を反対にたどっていけば対応する z が存在することがわかる。
よって、軌跡は、中心が $\dfrac{1}{\alpha}$ で、半径が $\dfrac{1}{|\alpha|}$ の円から、原点を取り除いたものになる。これから、求める円の中心は $\dfrac{1}{\alpha}$ 、半径は $\dfrac{1}{|\alpha|}$ である。
(2)
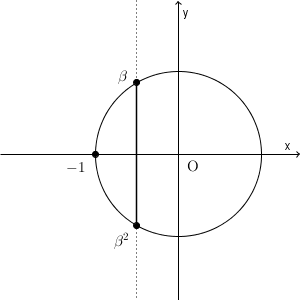
$\beta=\dfrac{-1+\sqrt{3}i}{2}$, $\beta^2=\dfrac{-1+\sqrt{3}i}{2}$ である。この2点を結ぶ線分は、点 $-1$ と原点とを結ぶ線分の垂直二等分線の一部なので、(1)と同じように計算すると、 w は
\begin{eqnarray}
\left| w+1 \right| &=& 1 \\[5pt]
\end{eqnarray}を満たすことがわかる。また、 z が垂直二等分線上にいるとき、2点を結ぶ線分の上だけを移動することは\[ |z|\leqq 1 \]が成り立つことと同値である。これは
\begin{eqnarray}
\left| \frac{1}{w} \right| &\leqq& 1 \\[5pt]
1 &\leqq& |w| \\[5pt]
\end{eqnarray}と同値である。よって、軌跡は、 $|w+1|=1$ の $|w|\geqq 1$ を満たす部分となる。図示すると次の太線部分(両端の点を含む)となる。
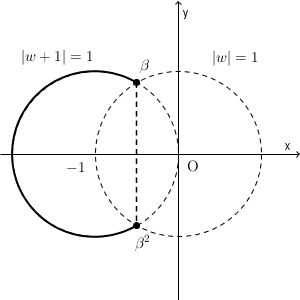
(終)
解説
(1)は、まず垂直二等分線を式で表します。円になるというヒントがあるので、 $|w-A|=B$ の形を目指して変形していきます。座標で考えるとこんなにスッキリとはいきません。
(2)は、(1)がヒントになっています。点 $-1$ と原点との垂直二等分線上にあるから、円の一部になることは(1)からわかります。垂直二等分線上で、線分上にあることと、原点からの距離が1以下であることが同値なので、この条件から円のどの部分が該当するかを求めています。





