東京大学 文系 2022年度 第1問 解説
問題編
問題
$a,b$ を実数とする。座標平面上の放物線 $y=x^2+ax+b$ を $C$ とおく。 $C$ は、原点で垂直に交わる2本の接線 $\ell_1,\ell_2$ を持つとする。ただし、 $C$ と $\ell_1$ の接点 $\mathrm{ P }_1$ の $x$ 座標は、 $C$ と $\ell_2$ の接点 $\mathrm{ P }_2$ の $x$ 座標より小さいとする。
(1) $b$ を $a$ で表せ。また $a$ の値はすべての実数をとりうることを示せ。
(2) $i=1,2$ に対し、円 $D_i$ を、放物線 $C$ の軸上に中心を持ち、点 $\mathrm{ P }_i$ で $\ell_i$ と接するものと定める。 $D_2$ の半径が $D_1$ の半径の2倍になるとき、 $a$ の値を求めよ。
考え方
接線から考え始めることもできるし、接点から考え始めることもできるでしょう。
(2)は、全部計算でやってしまうよりも、図形的な性質を使って計算量を減らした方がいいでしょう。
解答編
問題
$a,b$ を実数とする。座標平面上の放物線 $y=x^2+ax+b$ を $C$ とおく。 $C$ は、原点で垂直に交わる2本の接線 $\ell_1,\ell_2$ を持つとする。ただし、 $C$ と $\ell_1$ の接点 $\mathrm{ P }_1$ の $x$ 座標は、 $C$ と $\ell_2$ の接点 $\mathrm{ P }_2$ の $x$ 座標より小さいとする。
(1) $b$ を $a$ で表せ。また $a$ の値はすべての実数をとりうることを示せ。
解答
(1)
$f(x)=x^2+ax+b$ とすると、 $f'(x)=2x+a$ である。
点 $\mathrm{ P }_1,\mathrm{ P }_2$ の $x$ 座標を、それぞれ $p_1,p_2$ とする。このとき、接線 $\ell_1$ の方程式は\[ y-f(p_1) = (2p_1+a)(x-p_1) \]とかける。これが原点を通るとすると
\begin{eqnarray}
0-f(p_1) &=& (2p_1+a)(0-p_1) \\[5pt]
p_1^2+ap_1+b &=& 2p_1^2+ap_1 \\[5pt]
p_1^2 &=& b \\[5pt]
\end{eqnarray}が成り立つ必要がある。同様に $\ell_2$ について考えると、 $p_2^2=b$ が成り立つ必要がある。
これより、 $b\gt 0$ であることが必要で、このとき、 $p_1\lt p_2$ より、 $p_1=-\sqrt{b}$, $p_2=\sqrt{b}$ となる。
2つの接線は垂直に交わるので、傾き同士の積が $-1$ だから
\begin{eqnarray}
(2p_1+a)(2p_2+a) &=& -1 \\[5pt]
(-2\sqrt{b}+a)(2\sqrt{b}+a) &=& -1 \\[5pt]
a^2-4b &=& -1 \\[5pt]
b &=& \frac{a^2+1}{4} \\[5pt]
\end{eqnarray}となる。これが成り立つとき、 $b\gt 0$ が成り立つので、条件を満たす接線が存在することがわかる。
よって、 $b=\dfrac{a^2+1}{4}$ であり、 $a$ はすべての実数をとりうることが示せた。(終)
解答編 つづき
問題
(2) $i=1,2$ に対し、円 $D_i$ を、放物線 $C$ の軸上に中心を持ち、点 $\mathrm{ P }_i$ で $\ell_i$ と接するものと定める。 $D_2$ の半径が $D_1$ の半径の2倍になるとき、 $a$ の値を求めよ。
解答
(2)
\[ x^2+ax+b=\left(x+\frac{a}{2}\right)^2-\frac{a^2}{4}+b \]なので、放物線 $C$ の軸は $x=-\dfrac{a}{2}$ である。よって、点 $\mathrm{ P }_1$, $\mathrm{ P }_2$ からこの軸までの距離は、それぞれ、 $-\dfrac{a}{2}+\sqrt{b}$, $\sqrt{b}+\dfrac{a}{2}$ となる。
次に、直線 $\ell_2$ と $x$ 軸のなす角を $\theta$ とおく $(0^{\circ}\lt \theta \lt 90^{\circ})$ と、 $\tan\theta$ は $\ell_2$ の傾きである $2\sqrt{b}+a$ と一致する。
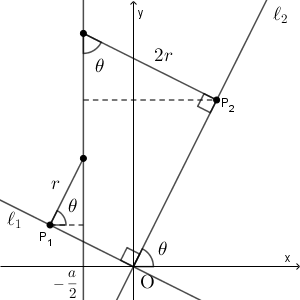
$\ell_1$ と $\ell_2$ が垂直に交わること、 $\ell_1$ が円 $D_1$ の接線であること、 $\ell_2$ が円 $D_2$ の接線であることから、円 $D_1$ の半径を $r$ とすると、点 $\mathrm{ P }_1$, $\mathrm{ P }_2$ からこの軸までの距離の比は
\begin{eqnarray}
r\cos\theta : 2r \sin\theta
&=&
1:2\tan\theta \\[5pt]
&=&
1:2(2\sqrt{b}+a) \\[5pt]
&=&
\frac{1}{4}:\left(\sqrt{b}+\dfrac{a}{2}\right) \\[5pt]
\end{eqnarray}となる。これが $\left(-\dfrac{a}{2}+\sqrt{b}\right):\left(\sqrt{b}+\dfrac{a}{2}\right)$ と一致するので\[ -\dfrac{a}{2}+\sqrt{b}=\frac{1}{4} \]が成り立つ。よって
\begin{eqnarray}
-2a+4\sqrt{\frac{a^2+1}{4} } &=& 1 \\[5pt]
\sqrt{4(a^2+1)} &=& 2a+1 \\[5pt]
\end{eqnarray}となる。左辺は正なので右辺も正である。両辺を2乗すると
\begin{eqnarray}
4(a^2+1) &=& (2a+1)^2 \\[5pt]
4a^2+4 &=& 4a^2+4a+1 \\[5pt]
4a &=& 3 \\[5pt]
a &=& \frac{3}{4} \\[5pt]
\end{eqnarray}となる。このとき $2a+1$ は正である。
よって、 $a=\dfrac{3}{4}$ (答)





