東京大学 文系 2018年度 第4問 解説
問題編
問題
放物線 $y=x^2$ のうち $-1\leqq x \leqq 1$ をみたす部分を C とする。座標平面上の原点 O と点 $\mathrm{ A }(1,0)$ を考える。
(1) 点 P が C 上を動くとき、\[ \overrightarrow{ \mathrm{ OQ } }=2\overrightarrow{ \mathrm{ OP } } \]を満たす点 Q の軌跡を求めよ。
(2) 点 P が C 上を動き、点 R が線分 OA 上を動くとき、\[ \overrightarrow{ \mathrm{ OS } }=2\overrightarrow{ \mathrm{ OP } }+\overrightarrow{ \mathrm{ OR } } \]をみたす点 S が動く領域を座標平面上に図示し、その面積を求めよ。
考え方
(1)は、 $\mathrm{ Q }(x,y)$ として、 $x,y$ が成り立つ式を考えればいいですね。
(2)は、式で考えるよりも、 $\overrightarrow{ \mathrm{ OR } }$ が加わった影響を考える方がいいでしょう。図形は対称性があるので、片方だけを計算します。
解答編
問題
放物線 $y=x^2$ のうち $-1\leqq x \leqq 1$ をみたす部分を C とする。座標平面上の原点 O と点 $\mathrm{ A }(1,0)$ を考える。
(1) 点 P が C 上を動くとき、\[ \overrightarrow{ \mathrm{ OQ } }=2\overrightarrow{ \mathrm{ OP } } \]を満たす点 Q の軌跡を求めよ。
(2) 点 P が C 上を動き、点 R が線分 OA 上を動くとき、\[ \overrightarrow{ \mathrm{ OS } }=2\overrightarrow{ \mathrm{ OP } }+\overrightarrow{ \mathrm{ OR } } \]をみたす点 S が動く領域を座標平面上に図示し、その面積を求めよ。
解答
(1)
$-1\leqq t \leqq 1$ とし、 $\overrightarrow{ \mathrm{ OP } }=(t,t^2)$ とおく。また、 $\overrightarrow{ \mathrm{ OQ } }=(x,y)$ とおく。
$\overrightarrow{ \mathrm{ OQ } }=2\overrightarrow{ \mathrm{ OP } }$ より、\[ x=2t,\ y=2t^2 \]が成り立つ。これより、 x の範囲は $-2\leqq x \leqq 2$ であることがわかる。また、
\begin{eqnarray}
y
&=&
2t^2 \\[5pt]
&=&
2\left(\frac{x}{2}\right)^2 \\[5pt]
&=&
\frac{1}{2}x^2 \\[5pt]
\end{eqnarray}となる。
以上から、点 Q の軌跡は、 $y=\dfrac{1}{2}x^2$ の $-2\leqq x \leqq 2$ の部分となる。
(2)
P を固定すると、 R が動くとき、 S は、点 P と P を x 軸方向に $1$ 移動した点との間を、 x 軸と平行な方向に動く。よって、 S の動く領域は、(1)で求めた図形を x 軸方向に $1$ 平行移動したときに通過する部分となるので、領域は以下の色のついた部分となる(境界線上の点を含む)。
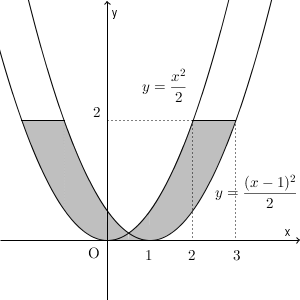
この部分は、 $x=\dfrac{1}{2}$ について対称なので、面積は
\begin{eqnarray}
& &
2\int_{\frac{1}{2} }^2 \frac{x^2}{2} dx +2\times 2\times 1 -2\int_1^3 \frac{(x-1)^2}{2} dx \\[5pt]
&=&
\int_{\frac{1}{2} }^2 x^2 dx +4 -\int_1^3 (x^2-2x+1) dx \\[5pt]
&=&
\left[\frac{x^3}{3}\right]_{\frac{1}{2} }^2 +4 -\left[\frac{x^3}{3}-x^2+x\right]_1^3 \\[5pt]
&=&
\frac{8}{3}-\frac{1}{24} +4 -(9-9+3)+\left(\frac{1}{3}-1+1\right) \\[5pt]
&=&
\frac{63}{24} +4 -3+\frac{1}{3} \\[5pt]
&=&
\frac{95}{24}
\end{eqnarray}と求められる。
(終)





