東京大学 文系 2018年度 第1問 解説
問題編
問題
座標平面上に放物線 C を\[ y=x^2-3x+4 \]で定め、領域 D を\[ y\geqq x^2-3x+4 \]で定める。原点をとおる2直線 l, m は C に接するものとする。
(1) 放物線 C 上を動く点 A と直線 l, m の距離をそれぞれ L, M とする。 $\sqrt{L}+\sqrt{M}$ が最小値をとるときの点 A の座標を求めよ。
(2) 次の条件をみたす点 $\mathrm{ P }(p,q)$ の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域 D のすべての点 $(x,y)$ に対し不等式 $px+qy\leqq 0$ が成り立つ。
考え方
(1)は、はじめはよくわからないですが、計算していくと $\sqrt{L}+\sqrt{M}$ が考えやすい式になることがわかります。グラフをかくのも、それほど大変ではありません。
(2)は、 $\dfrac{y}{x}$ と $\dfrac{q}{p}$ に分けて考えたほうがわかりやすいと思います。l, m の式から $\dfrac{y}{x}$ のとり得る値がわかるので、これを利用しましょう。
解答編
問題
座標平面上に放物線 C を\[ y=x^2-3x+4 \]で定め、領域 D を\[ y\geqq x^2-3x+4 \]で定める。原点をとおる2直線 l, m は C に接するものとする。
(1) 放物線 C 上を動く点 A と直線 l, m の距離をそれぞれ L, M とする。 $\sqrt{L}+\sqrt{M}$ が最小値をとるときの点 A の座標を求めよ。
(2) 次の条件をみたす点 $\mathrm{ P }(p,q)$ の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域 D のすべての点 $(x,y)$ に対し不等式 $px+qy\leqq 0$ が成り立つ。
解答
(1)
$f(x)=x^2-3x+4$ とする。 $f'(x)=2x-3$ なので、 $y=f(x)$ の $(t,f(t))$ における接線の方程式は
\begin{eqnarray}
y
&=&
(2t-3)(x-t)+(t^2-3t+4) \\[5pt]
&=&
(2t-3)x -2t^2+3t +t^2-3t+4 \\[5pt]
&=&
(2t-3)x -t^2+4 \\[5pt]
\end{eqnarray}となる。よって、これが原点と通るとき、 $t=\pm 2$ となる。このことから、 $l,m$ は、 $y=x$ と $y=-7x$ である。
点 A の座標を $(a,f(a))$ とすると、点 A と直線 $y=x$ との距離は
\begin{eqnarray}
\frac{|(a^2-3a+4)-a|}{\sqrt{1+1} } &=& \frac{|(a-2)^2|}{\sqrt{2} }
\end{eqnarray}となる。また、点 A と直線 $y=-7x$ との距離は
\begin{eqnarray}
\frac{|(a^2-3a+4)-(-7a)|}{\sqrt{1+49} } &=& \frac{|(a+2)^2|}{5\sqrt{2} }
\end{eqnarray}となる。よって、
\begin{eqnarray}
\sqrt{L}+\sqrt{M}
&=&
\frac{1}{\sqrt[ 4 ]{ 2 } } |a-2|+\frac{1}{\sqrt{5}\sqrt[ 4 ]{ 2 } } |a+2| \\[5pt]
&=&
\frac{1}{\sqrt{5}\sqrt[ 4 ]{ 2 } } \left( \sqrt{5}|a-2|+|a+2|\right) \\[5pt]
\end{eqnarray}となる。このことから、 $\sqrt{5}|a-2|+|a+2|$ が最小となるときを求めればよい。
(ア) $a\lt -2$ のとき
\begin{eqnarray}
\sqrt{5}|a-2|+|a+2|
&=&
\sqrt{5}(-a+2)+(-a-2) \\[5pt]
&=&
(-\sqrt{5}-1)a +2\sqrt{5}-2 \\[5pt]
\end{eqnarray}
(イ) $-2\leqq a\lt 2$ のとき
\begin{eqnarray}
\sqrt{5}|a-2|+|a+2|
&=&
\sqrt{5}(-a+2)+(a+2) \\[5pt]
&=&
(-\sqrt{5}+1)a +2\sqrt{5}+2 \\[5pt]
\end{eqnarray}
(ウ) $a\geqq 2$ のとき
\begin{eqnarray}
\sqrt{5}|a-2|+|a+2|
&=&
\sqrt{5}(a-2)+(a+2) \\[5pt]
&=&
(\sqrt{5}+1)a -2\sqrt{5}+2 \\[5pt]
\end{eqnarray}
(ア)(イ)(ウ)と $\sqrt{5}\gt 1$ より、 $y=\sqrt{5}|a-2|+|a+2|$ のグラフは以下のようになる。
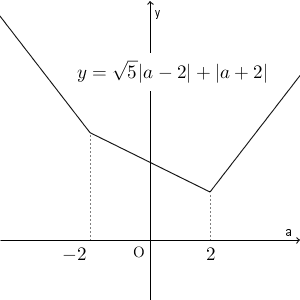
よって、 $\sqrt{5}|a-2|+|a+2|$ が最小となるのは $a=2$ のときである。 $f(2)=2$ なので、このときの点 A の座標は\[ (2,2) \]となる。
(2)
$q\gt 0$ とすると
\begin{eqnarray}
& & px+qy \leqq 0 \\[5pt]
&\iff& y \leqq -\frac{p}{q}x \\[5pt]
\end{eqnarray}である。点 $(x,y)$ が領域 D 内にあるとすると、 x はすべての実数値を取り得、 y はつねに正の値をとるため、この不等式が成り立つことはない。
$q=0$ とすると
\begin{eqnarray}
& & px+qy \leqq 0 \\[5pt]
&\iff& px \leqq 0 \\[5pt]
\end{eqnarray}である。点 $(x,y)$ が領域 D 内にあるとき、 x はすべての実数値をとりえるため、条件を満たすのは\[ p=0 \] のときであることがわかる。
以下では、 $q\lt 0$ のときを考える。(1)より、領域 D と2直線 l, m のグラフは次の通りとなる。

$x\gt 0$ のときは、
\begin{eqnarray}
& & px+qy \leqq 0 \\[5pt]
&\iff& \frac{y}{x} \geqq -\frac{p}{q} \\[5pt]
\end{eqnarray}である。ここで、上のグラフより、 $x\gt 0$ の範囲では $\dfrac{y}{x}$ は $1$ 以上のすべての値をとる。よって、条件を満たすことは
\begin{eqnarray}
1 \geqq -\frac{p}{q} \\[5pt]
q \leqq -p \\[5pt]
\end{eqnarray}と同値である。
$x=0$ のときは
\begin{eqnarray}
& & px+qy \leqq 0 \\[5pt]
&\iff& qy \leqq 0 \\[5pt]
\end{eqnarray}である。今考えているのは $q\lt 0$ のときであり、領域 D 内の点 $(x,y)$ について、 $y\gt 0$ が成り立つので、この場合はつねに不等式が成り立つ。
$x\lt 0$ のときは、
\begin{eqnarray}
& & px+qy \leqq 0 \\[5pt]
&\iff& \frac{y}{x} \leqq -\frac{p}{q} \\[5pt]
\end{eqnarray}である。ここで、上のグラフより、 $x\lt 0$ の範囲では $\frac{y}{x}$ は $-7$ 以下のすべての値をとる。よって、条件を満たすことは
\begin{eqnarray}
-7 \leqq -\frac{p}{q} \\[5pt]
-7q \geqq -p \\[5pt]
q \leqq \frac{1}{7}p \\[5pt]
\end{eqnarray}と同値である。
以上より、条件を満たす $\mathrm{ P }(p,q)$ は
- $(0,0)$
- $q\lt 0$ かつ $q \leqq -p$ かつ $q \leqq \dfrac{1}{7}p$ を満たす点
この範囲を図示すると以下の斜線部分(境界線上の点を含む)となる。

これより、求める範囲は、「 $q \leqq -p$ かつ $q \leqq \dfrac{1}{7}p$ を満たす点 $(p,q)$ 全体」となる。
(終)





