東京大学 文系 2017年度 第2問 解説
問題編
問題
1辺の長さが $1$ の正六角形 ABCDEF が与えられている。点 P が辺 AB 上を、点 Q が辺 CD 上をそれぞれ独立に動くとき、線分 PQ を $2:1$ に内分する点 R が通りうる範囲の面積を求めよ。
考え方
まずは R の動く範囲を求めましょう。ベクトルを使えば求めやすいです。正六角形なので、等しいベクトルがいくつもあり、扱いやすいです。動く範囲が分かれば、同じ形の図形の面積を求めれば終了です。
解答編
問題
1辺の長さが $1$ の正六角形 ABCDEF が与えられている。点 P が辺 AB 上を、点 Q が辺 CD 上をそれぞれ独立に動くとき、線分 PQ を $2:1$ に内分する点 R が通りうる範囲の面積を求めよ。
解答
$\overrightarrow{ \mathrm{ AB } }=\overrightarrow{ a }$, $\overrightarrow{ \mathrm{ AF } }=\overrightarrow{ b }$ とおく。また、 $\mathrm{ AP }=p$, $\mathrm{ CQ }=q$ とする( $0 \leqq p,q \leqq 1$ )。AD と BE の交点を O とする。
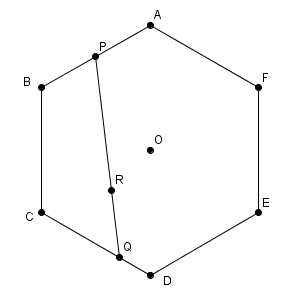
$\overrightarrow{ \mathrm{ AP } }=p\overrightarrow{ a }$ である。また、
\begin{eqnarray}
\overrightarrow{ \mathrm{ AQ } }
&=&
\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BC } }+\overrightarrow{ \mathrm{ CQ } } \\[5pt]
&=&
\overrightarrow{ a }+(\overrightarrow{ \mathrm{ AB } }+\overrightarrow{ \mathrm{ BO } })+q\overrightarrow{ b } \\[5pt]
&=&
\overrightarrow{ a }+(\overrightarrow{ a }+\overrightarrow{ b })+q\overrightarrow{ b } \\[5pt]
&=&
2\overrightarrow{ a }+(1+q)\overrightarrow{ b } \\[5pt]
\end{eqnarray}となる。よって
\begin{eqnarray}
\overrightarrow{ \mathrm{ AR } }
&=&
\frac{\overrightarrow{ \mathrm{ AP } }+2\overrightarrow{ \mathrm{ AQ } } }{3} \\[5pt]
&=&
\frac{p\overrightarrow{ a }+2\left\{2\overrightarrow{ a }+(1+q)\overrightarrow{ b }\right\} }{3} \\[5pt]
&=&
\frac{4+p}{3}\overrightarrow{ a }+\frac{2+2q}{3}\overrightarrow{ b } \\[5pt]
\end{eqnarray}となる。 p, q は $0\leqq p,q \leqq 1$ を満たしながら独立に動くため、
\begin{eqnarray}
\overrightarrow{ \mathrm{ AG } } &=& \frac{4}{3}\overrightarrow{ a }+\frac{2}{3}\overrightarrow{ b } \\[5pt]
\overrightarrow{ \mathrm{ AH } } &=& \frac{5}{3}\overrightarrow{ a }+\frac{2}{3}\overrightarrow{ b } \\[5pt]
\overrightarrow{ \mathrm{ AI } } &=& \frac{5}{3}\overrightarrow{ a }+\frac{4}{3}\overrightarrow{ b } \\[5pt]
\overrightarrow{ \mathrm{ AJ } } &=& \frac{4}{3}\overrightarrow{ a }+\frac{4}{3}\overrightarrow{ b } \\[5pt]
\end{eqnarray}となる点 G, H, I, J をとると、 R の動く範囲は、平行四辺形 GHIJ の周と内部となる。
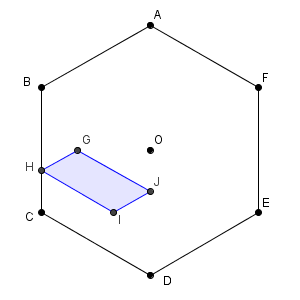
これは、辺の長さが $\dfrac{|\overrightarrow{ a }|}{3}, \dfrac{2|\overrightarrow{ b }|}{3}$ だけからなる、1つの角が $60^{\circ}$ の平行四辺形なので、この面積は
\begin{eqnarray}
\frac{1}{3} \times \frac{2}{3} \times \sin 60^{\circ} =\frac{\sqrt{3} }{9}
\end{eqnarray}となる。
(終)
解説
R をベクトルで表して、動く範囲を求めます。ベクトルの基準は A としましたが、どこでも構いません。
動く範囲が求められれば、辺の長さと角度は分かるので、面積もすぐに求められます。





