東京大学 文系 2013年度 第3問 解説
問題編
問題
$a,b$ を実数の定数とする。実数 $x,y$ が\[ x^2+y^2\leqq 25,\ 2x+y\leqq 5 \]をともに満たすとき、 $z=x^2+y^2-2ax-2by$ の最小値を求めよ。
考え方
何を考えるべきかはわかりやすいですが、解答をどこまで細かく書くかは悩ましいです。場合分けがたくさんあるので大変ですが、どういうときに最小になるかを考えれば、どのように分けるべきかは思いつきやすいでしょう。
解答編
問題
$a,b$ を実数の定数とする。実数 $x,y$ が\[ x^2+y^2\leqq 25,\ 2x+y\leqq 5 \]をともに満たすとき、 $z=x^2+y^2-2ax-2by$ の最小値を求めよ。
解答
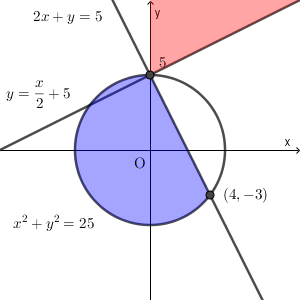
連立不等式 $x^2+y^2\leqq 25$, $2x+y\leqq 5$ の表す領域を $D$ とおき、点 $\mathrm{P}(x,y)$ はこの領域(境界線上の点を含む)内の点とする。また、点 $\mathrm{A}(a,b)$ とする。
$x^2+y^2=25$, $2x+y=5$ の交点の $x$ 座標は
\begin{eqnarray}
x^2+(5-2x)^2 &=& 25 \\[5pt]
x^2+4x^2-20x+25 &=& 25 \\[5pt]
x(x-4) &=& 0 \\[5pt]
x &=& 0,4
\end{eqnarray}なので、交点の座標は $(0,5)$, $(4,-3)$ である。よって、領域 $D$ は次の図の色のついた部分(境界上の点を含む)となる。
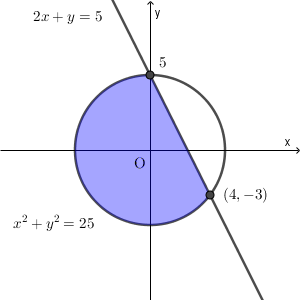
$(a,b)$ が
$a^2+b^2\leqq 25$ かつ $2x+y\leqq 5$
を満たすとき、点A は領域 $D$ 内にあるので、 点 P が点 A と同じ場所にあるときに $z$ が最小となり、その値は $-a^2-b^2$ である。
以下では、点A が領域 $D$ の外側にあるときを考える。
点 S を、領域 $D$ の内部(境界線上の点を除く)の点とする。領域 $D$ の境界線と線分 AS との交点を T とすると、 AT は AS より短い。
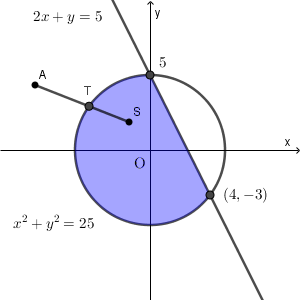
このことから、点 A が領域 $D$ の外側にあるとき、線分 AP が最小になる場合を考えるには、 点 P が領域 $D$ の境界線上にある場合だけを考えればよい。
一般に、点 C を中心にした円 $C$ とこの円の外部の点 E があり、点 B が円 $C$ の円周を動くとき、BE が最小になるのは、点 B が円 $C$ の円周と線分 CE との交点にあるときである。

よって、線分 AO と円 $x^2+y^2=25$ との共有点が領域 $D$ にあるときは、点 $(x,y)$ がその共有点のときに $z$ が最小となる。
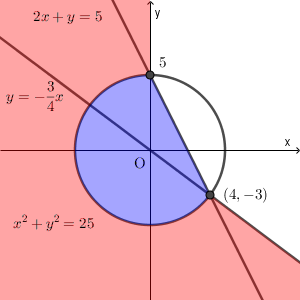
このようになるのは、
$a^2+b^2\gt 25$ かつ 「 $a\leqq 0$ または $b\leqq -\dfrac{3}{4}a$ 」
のときである。このとき、領域 $D$ と点 A との距離は、線分 AO の長さから $5$ を引いたものなので、
\begin{eqnarray}
z
&=&
(\sqrt{a^2+b^2}-5)^2-a^2-b^2 \\[5pt]
&=&
-10\sqrt{a^2+b^2}+25 \\[5pt]
\end{eqnarray}となる。
また、点 A から直線 $2x+y=0$ に垂線をおろし、その足が領域 $D$ の境界線上にあるときは、点 P がその点のときに $z$ が最小となる。
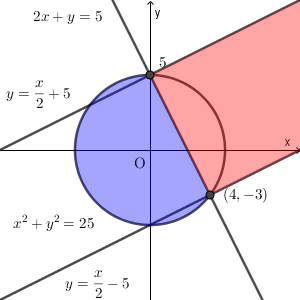
$2x+y=5$ に垂直な線の傾きは $\dfrac{1}{2}$ である。よって、 $2x+y=5$ に垂直で点 $(0,5)$ を通る直線の方程式は $y=\dfrac{1}{2}x+5$ であり、点 $(4,-3)$ を通る直線の方程式は $y=\dfrac{1}{2}x-5$ である。以上から、
$2a+b\gt 5$ かつ $b\leqq \dfrac{1}{2}a+5$ かつ $b\geqq \dfrac{1}{2}a-5$
のとき、領域 $D$ と点 A との距離は、点 A と直線 $2x+y=5$ との距離に一致するので
\begin{eqnarray}
z
&=&
\left(\frac{2a+b-5}{\sqrt{2^2+1^2} }\right)^2-a^2-b^2 \\[5pt]
&=&
\frac{4a^2+b^2+25+4ab-20a-10b}{5}-a^2-b^2 \\[5pt]
&=&
\dfrac{-a^2+4ab-4b^2}{5}+5-4a-2b \\[5pt]
\end{eqnarray}となる。
まだ考えていないケースのうち、点 A が次の領域にある場合を考える(境界線上の点を除く)。
この領域は
$a\gt 0$ かつ $b\gt\dfrac{1}{2}a+5$
であり、点 A がこの領域にある場合、点 P が $(0,5)$ にあるときに AP の長さが最小になる。よって、
\begin{eqnarray}
z
&=&
a^2+(b-5)^2-a^2-b^2 \\[5pt]
&=&
-10b+25 \\[5pt]
\end{eqnarray}となる。
残っているのは、点 A が次の領域にある場合である(境界線上の点を除く)。
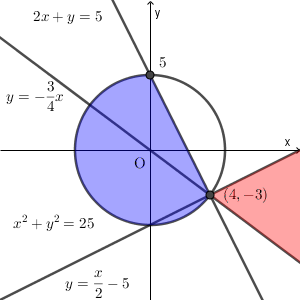
この領域は
$b\gt -\dfrac{3}{4}a$ かつ $b\lt\dfrac{1}{2}a-5$
であり、点 A がこの領域にある場合、点 P が $(4,-3)$ にあるときに AP の長さが最小になる。よって、
\begin{eqnarray}
z
&=&
(a-4)^2+(b+3)^2-a^2-b^2 \\[5pt]
&=&
-8a+6b+25 \\[5pt]
\end{eqnarray}となる。
以上から、 $z$ の最小値は以下のようになる。
(1) $a^2+b^2\leqq 25$ かつ $2x+y\leqq 5$ のとき
$-a^2-b^2$
(2) $a^2+b^2\gt 25$ かつ 「 $a\leqq 0$ または $b\leqq -\dfrac{3}{4}a$ 」のとき
$-10\sqrt{a^2+b^2}+25$
(3) $2a+b\gt 5$ かつ $b\leqq \dfrac{1}{2}a+5$ かつ $b\geqq \dfrac{1}{2}a-5$ のとき
$\dfrac{-a^2+4ab-4b^2}{5}+5-4a-2b$
(4) $a\gt 0$ かつ $b\gt\dfrac{1}{2}a+5$ のとき
$-10b+25$
(5) $b\gt -\dfrac{3}{4}a$ かつ $b\lt\dfrac{1}{2}a-5$ のとき
$-8a+6b+25$
(解答終)
解説
解答に書いた(1)~(5)を色分けして表示すると次のようになります。
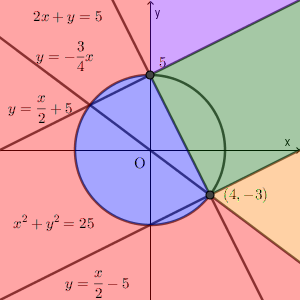
(1)が青、(2)が赤、(3)が緑、(4)が紫、(5)が黄に対応しています。





