東京大学 文系 2013年度 第2問 解説
問題編
問題
座標平面上の3点
\begin{eqnarray} & & \mathrm{P}(0,-\sqrt{2}), \\[5pt] & & \mathrm{Q}(0, \sqrt{2}), \\[5pt] & & \mathrm{A}(a, \sqrt{a^2+1})\quad (0\leqq a\leqq 1) \end{eqnarray}を考える。(1) 2つの線分の長さの差 $\mathrm{PA}-\mathrm{AQ}$ は $a$ によらない定数であることを示し、その値を求めよ。
(2) $\mathrm{Q}$ を端点とし $\mathrm{A}$ を通る半直線と放物線 $y=\dfrac{\sqrt{2} }{8}x^2$ との交点を $\mathrm{B}$ とする。点 $\mathrm{B}$ から直線 $y=2$ へ下した垂線と直線 $y=2$ との交点を $\mathrm{C}$ とする。このとき、線分の長さの和\[ \mathrm{PA+AB+BC} \]は $a$ によらない定数であることを示し、その値を求めよ。
考え方
三平方の定理を使って計算するくらいしかないので、やるべきことはすぐにわかります。しかし、その計算がやたらと大変です。
「定数になる」のだから、値だけを求めるなら簡単です( $a$ にわかりやすい値を入れて求めればいいです)。ただ、答えがわかっても、大したヒントにはなりません。根号の計算を頑張っていくしかありません。
ちなみに、数学IIIをやった人(理系の人など)なら、これは双曲線や放物線と焦点との距離を考えているんだな、ということがわかるでしょう。これらの性質から、問題文にある線分の差や和が一定になることもわかります。ただ、それがわかったとしても、それ自体を計算で示さないといけないのだから、「数学IIIをやっていたから有利」というほどでもないでしょう。
(2)では(1)を使いますが、(2)のほうが根号の計算自体はやさしめです。ただ、はまってしまうポイントもあるので注意です。
$a$ に好きな値を入れて検算ができるので、最後に確認しましょう。
解答編
問題
座標平面上の3点
\begin{eqnarray} & & \mathrm{P}(0,-\sqrt{2}), \\[5pt] & & \mathrm{Q}(0, \sqrt{2}), \\[5pt] & & \mathrm{A}(a, \sqrt{a^2+1})\quad (0\leqq a\leqq 1) \end{eqnarray}を考える。(1) 2つの線分の長さの差 $\mathrm{PA}-\mathrm{AQ}$ は $a$ によらない定数であることを示し、その値を求めよ。
解答
(1)
\begin{eqnarray}
& &
\mathrm{PA} \\[5pt]
&=&
\sqrt{a^2+(\sqrt{a^2+1}+\sqrt{2})^2} \\[5pt]
&=&
\sqrt{a^2+a^2+1+2\sqrt{2a^2+2}+2} \\[5pt]
&=&
\sqrt{2a^2+3+2\sqrt{2a^2+2} } \\[5pt]
&=&
\sqrt{(\sqrt{2a^2+2}+1)^2} \\[5pt]
&=&
\sqrt{2a^2+2}+1 \\[5pt]
\end{eqnarray}となる。また、
\begin{eqnarray}
& &
\mathrm{AQ} \\[5pt]
&=&
\sqrt{a^2+(\sqrt{a^2+1}-\sqrt{2})^2} \\[5pt]
&=&
\sqrt{2a^2+3-2\sqrt{2a^2+2} } \\[5pt]
&=&
\sqrt{(\sqrt{2a^2+2}-1)^2} \\[5pt]
\end{eqnarray}となる。 $\sqrt{2a^2+2}\geqq \sqrt{2}\gt 1$ なので、\[ \mathrm{AQ}=\sqrt{2a^2+2}-1 \]となるので、
\begin{eqnarray}
& &
\mathrm{PA}-\mathrm{AQ} \\[5pt]
&=&
(\sqrt{2a^2+2}+1)-(\sqrt{2a^2+2}-1) \\[5pt]
&=&
2
\end{eqnarray}となる。よって、 $\mathrm{PA}-\mathrm{AQ}$ は、 $2$ であり、 $a$ の値によらない定数である。
((1)終)
解答編 つづき
問題
(2) $\mathrm{Q}$ を端点とし $\mathrm{A}$ を通る半直線と放物線 $y=\dfrac{\sqrt{2} }{8}x^2$ との交点を $\mathrm{B}$ とする。点 $\mathrm{B}$ から直線 $y=2$ へ下した垂線と直線 $y=2$ との交点を $\mathrm{C}$ とする。このとき、線分の長さの和\[ \mathrm{PA+AB+BC} \]は $a$ によらない定数であることを示し、その値を求めよ。
解答
(2)
3点 $\mathrm{Q, A, B}$ は、点の取り方から、 $\mathrm{Q, A, B}$ の順に並んでいるか $\mathrm{Q, B, A}$ の順に並んでいるかのどちらかの場合しかない。ところが、実際には $\mathrm{Q, A, B}$ の順に並んでいる場合しかない。まずは、このことを示す。
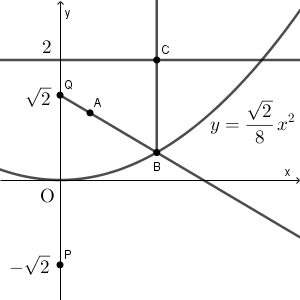
(1)より、 $\mathrm{QA}=\sqrt{2a^2+2}-1\leqq \sqrt{2+2}-1=1$ である。一方、点 $\mathrm{B}$ の $x$ 座標を $b$ とすると、
\begin{eqnarray}
& &
\mathrm{QB} \\[5pt]
&=&
\sqrt{b^2 +\left(\frac{\sqrt{2} }{8}b^2-\sqrt{2}\right)^2} \\[5pt]
&=&
\sqrt{b^2 +\frac{b^4}{32} -2\cdot\frac{\sqrt{2} }{8}b^2\cdot\sqrt{2} +2} \\[5pt]
&=&
\sqrt{\frac{b^4}{32} +\frac{b^2}{2} +2} \\[5pt]
&=&
\sqrt{\frac{b^4+16b^2+64}{32} } \\[5pt]
&=&
\frac{b^2+8}{4\sqrt{2} } \\[5pt]
\end{eqnarray}なので、 $\mathrm{QB}\geqq \dfrac{0+8}{4\sqrt{2} }=\sqrt{2}$ である。よって、 $\mathrm{QB}\gt \mathrm{QA}$ だから、 $\mathrm{Q, A, B}$ の順に並んでいる場合しかない。
このとき、 $\mathrm{QB=QA+AB}$ なので、
\begin{eqnarray}
& &
\mathrm{PA}+\mathrm{AB}+\mathrm{BC} \\[5pt]
&=&
2+\mathrm{QA}+\mathrm{AB}+\mathrm{BC} \\[5pt]
&=&
2+\mathrm{QB}+\mathrm{BC} \\[5pt]
\end{eqnarray}である。 $\mathrm{A}$ の $y$ 座標 $\sqrt{a^2+1}$ は、 $\mathrm{Q}$ の $y$ 座標 $\sqrt{2}$ より大きくなることはないので、 $\mathrm{B}$ の $y$ 座標も $\sqrt{2}$ より大きくなることはない。よって、 $\mathrm{BC}=2-\frac{\sqrt{2} }{8}b^2$ なので、
\begin{eqnarray}
& &
2+\mathrm{QB}+\mathrm{BC} \\[5pt]
&=&
2+\frac{b^2+8}{4\sqrt{2} }+2-\frac{\sqrt{2} }{8}b^2 \\[5pt]
&=&
4+\sqrt{2} \\[5pt]
\end{eqnarray}
となる。よって、 $\mathrm{PA}+\mathrm{AB}+\mathrm{BC}$ は $4+\sqrt{2}$ であり、 $a$ の値によらない定数である。
((2)終)
解説
A の座標から B の座標を求める、とやりだすと、答えにたどりつくのは相当難しいでしょう。
$a=0,1$ のときを考えると、 Q, A, B の順に並ぶのではないか、と予想できます。さらに(1)の結果も使えば、 A が式から消え、 B の $x$ 座標だけで表すことができるようになります。
これらのことに気づくのは大変ですが、ここがクリアできれば、二重根号をはずすのは(1)に比べるとそんなに大変ではありません。





