共通テスト 数学II・数学B 2024年度追試 第5問 解説
【第3問~第5問から2問選択】
問題編
問題
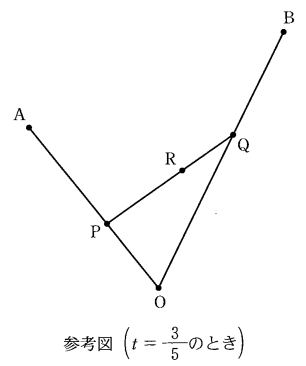
平面上に3点 $\mathrm{O,A,B}$ がある。ただし、 $\mathrm{O,A,B}$ は同一直線上にはないとする。 $\vec{a}=\overrightarrow{\mathrm{OA}}$, $\vec{b}=\overrightarrow{\mathrm{OB}}$ とおく。
$t$ を $0\lt t\lt 1$ を満たす実数とし、3点 $\mathrm{P,Q,R}$ を以下のように定める。
・線分 $\mathrm{OA}$ を $(1-t):t$ に内分する点を $\mathrm{P}$ とする。
・線分 $\mathrm{OB}$ を $t:(1-t)$ に内分する点を $\mathrm{Q}$ とする。
・線分 $\mathrm{PQ}$ を $t:(1-t)$ に内分する点を $\mathrm{R}$ とする。
(1) $\overrightarrow{\mathrm{OP}}$, $\overrightarrow{\mathrm{OQ}}$, $\overrightarrow{\mathrm{OR}}$ を $\vec{a}$, $\vec{b}$ と $t$ を用いて表すと
\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& \dBox{ア} \vec{a} \\[5pt] \overrightarrow{\mathrm{OQ}} &=& \dBox{イ} \vec{b} \\[5pt] \overrightarrow{\mathrm{OR}} &=& \dBox{ウ} \vec{a}+\dBox{エ} \vec{b} \\[5pt] \end{eqnarray}である。$\dbox{ア}$ ~ $\dbox{エ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $t$
1: $(t-1)$
2: $(1-t)$
3: $(-t)$
4: $t^2$
5: $t(1-t)$
6: $2t(1-t)$
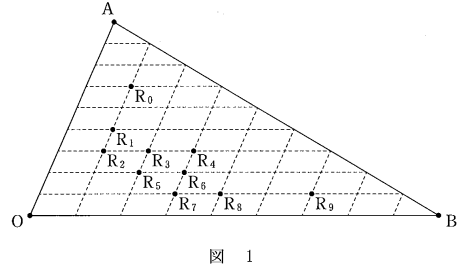
7: $(1-t)^2$(2) $\mathrm{O,A,B}$ を図1の位置にとる。 $t=\frac{1}{3}$ のときの $\mathrm{R}$ の位置について、図1における点 $\mathrm{R}_0,\mathrm{R}_1,\cdots,\mathrm{R}_9$ のうち正しいものは $\dBox{オ}$ である。ただし、図1における破線は、 $\mathrm{OA}$ を9等分する点を通り $\mathrm{OB}$ に平行な線分と、 $\mathrm{OB}$ を9等分する点を通り $\mathrm{OA}$ に平行な線分である。また、 $\mathrm{R}_0,\mathrm{R}_1,\cdots,\mathrm{R}_9$ は、いずれもこれらの線分どうしの交点である。
$\dbox{オ}$ の解答群
0: $\mathrm{R}_0$
1: $\mathrm{R}_1$
2: $\mathrm{R}_2$
3: $\mathrm{R}_3$
4: $\mathrm{R}_4$
5: $\mathrm{R}_5$
6: $\mathrm{R}_6$
7: $\mathrm{R}_7$
8: $\mathrm{R}_8$
9: $\mathrm{R}_9$(3) $0^{\circ}\lt \angle \mathrm{AOB}\lt 90^{\circ}$ の場合を考える。 $\overrightarrow{\mathrm{OC}}=\vec{a}+\vec{b}$ を満たす点 $\mathrm{C}$ をとる。 $\mathrm{O}$ を通り直線 $\mathrm{OC}$ と垂直に交わる直線を $\ell$ とする。 $t$ が $0\lt t\lt 1$ の範囲を動くとき、 $\mathrm{R}$ と $\ell$ の距離について考えよう。
直線 $\mathrm{BC}$ と $\ell$ の交点を $\mathrm{D}$ とし、 $k$ を $\mathrm{OA:BD}=1:k$ を満たす正の数とする。
(i) $\overrightarrow{\mathrm{OD}}$ を $\vec{a},\vec{b}$ と $k$ を用いて表すと\[ \overrightarrow{\mathrm{OD}}=\dBox{カ} \]である。また、直線 $\mathrm{OC}$ と直線 $\mathrm{OD}$ が垂直に交わることから、 $k=\dBox{キ}$ であることがわかる。
$\dbox{カ}$ の解答群
0: $k\vec{a}+\vec{b}$
1: $k\vec{a}-\vec{b}$
2: $-k\vec{a}+\vec{b}$
3: $-k\vec{a}-\vec{b}$
4: $\vec{a}+k\vec{b}$
5: $\vec{a}-k\vec{b}$
6: $-\vec{a}+k\vec{b}$
7: $-\vec{a}-k\vec{b}$
$\dbox{キ}$ の解答群
0: $\dfrac{|\vec{a}|}{|\vec{b}|}$
1: $\dfrac{|\vec{b}|}{|\vec{a}|}$
2: $\dfrac{|\vec{a}|^2+\vec{a}\cdot\vec{b}}{|\vec{b}|^2+\vec{a}\cdot\vec{b}}$
3: $\dfrac{-|\vec{a}|^2-\vec{a}\cdot\vec{b}}{|\vec{b}|^2+\vec{a}\cdot\vec{b}}$
4: $\dfrac{|\vec{b}|^2+\vec{a}\cdot\vec{b}}{|\vec{a}|^2+\vec{a}\cdot\vec{b}}$
5: $\dfrac{-|\vec{b}|^2-\vec{a}\cdot\vec{b}}{|\vec{a}|^2+\vec{a}\cdot\vec{b}}$
(ii) $\vec{c}=\overrightarrow{\mathrm{OC}}$, $\vec{d}=\overrightarrow{\mathrm{OD}}$ とおく。 $\overrightarrow{\mathrm{OR}}$ を、垂直な二つのベクトル $\vec{c},\vec{d}$ と $k,t$ を用いて表すことを考えよう。まず $\vec{a}$ と $\vec{b}$ は、 $\vec{c},\vec{d}$ と $k$ を用いると\[ \vec{a}=\dfrac{1}{k+1}\left(\dBox{ク}\right),\ \vec{b}=\dfrac{1}{k+1}\left(\dBox{ケ}\right) \]と表すことができる。
これから
\begin{eqnarray} \overrightarrow{\mathrm{OR}} &=& \frac{1}{k+1}\left\{\dBox{コ}t^2-\dBox{サ}t+\dBox{シ}\right\}\vec{c} \\[5pt] & & +\frac{1}{k+1}\left(\dBox{ス}-\dBox{セ}\right)\vec{d} \end{eqnarray}であることがわかる。$\dbox{ク},\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\vec{c}+\vec{d}$
1: $\vec{c}-\vec{d}$
2: $-\vec{c}+\vec{d}$
3: $k\vec{c}+\vec{d}$
4: $\vec{c}+k\vec{d}$
$\dbox{コ}$ ~ $\dbox{セ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\frac{1}{2}$
1: $1$
2: $2$
3: $k$
4: $2k$
5: $(k+1)$
6: $2(k+1)$
7: $(k-1)$
8: $2(k-1)$
(iii) $t$ が $0\lt t\lt 1$ の範囲を動くとき、 $\mathrm{R}$ と $\ell$ の距離が最小になるのは $t=\dBox{ソ}$ のときである。
$\dbox{ソ}$ の解答群
0: $\dfrac{1}{2}$
1: $\dfrac{1}{k-1}$
2: $\dfrac{2}{k-1}$
3: $\dfrac{1}{k}$
4: $\dfrac{2}{k}$
5: $\dfrac{k-1}{k}$
6: $\dfrac{1}{k+1}$
7: $\dfrac{2}{k+1}$
8: $\dfrac{k-1}{k+1}$
9: $\dfrac{k}{k+1}$
考え方
(2)は少し目新しいですが、式の形を見て考えましょう。 $\mathrm{R}$ の定義から考えても解けるので、ベクトルの問題と思わずに解くこともできてしまいます。
(3)(ii)は、そこまでに出てきた式を組み合わせて解きましょう。(iii)は、(ii)の答えのどこに注目すればいいかを考えます。なんのためにこのような式で表したのかを考えてみましょう。
【第3問~第5問から2問選択】
解答編
問題
平面上に3点 $\mathrm{O,A,B}$ がある。ただし、 $\mathrm{O,A,B}$ は同一直線上にはないとする。 $\vec{a}=\overrightarrow{\mathrm{OA}}$, $\vec{b}=\overrightarrow{\mathrm{OB}}$ とおく。
$t$ を $0\lt t\lt 1$ を満たす実数とし、3点 $\mathrm{P,Q,R}$ を以下のように定める。
・線分 $\mathrm{OA}$ を $(1-t):t$ に内分する点を $\mathrm{P}$ とする。
・線分 $\mathrm{OB}$ を $t:(1-t)$ に内分する点を $\mathrm{Q}$ とする。
・線分 $\mathrm{PQ}$ を $t:(1-t)$ に内分する点を $\mathrm{R}$ とする。
(1) $\overrightarrow{\mathrm{OP}}$, $\overrightarrow{\mathrm{OQ}}$, $\overrightarrow{\mathrm{OR}}$ を $\vec{a}$, $\vec{b}$ と $t$ を用いて表すと
\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& \dBox{ア} \vec{a} \\[5pt] \overrightarrow{\mathrm{OQ}} &=& \dBox{イ} \vec{b} \\[5pt] \overrightarrow{\mathrm{OR}} &=& \dBox{ウ} \vec{a}+\dBox{エ} \vec{b} \\[5pt] \end{eqnarray}である。$\dbox{ア}$ ~ $\dbox{エ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $t$
1: $(t-1)$
2: $(1-t)$
3: $(-t)$
4: $t^2$
5: $t(1-t)$
6: $2t(1-t)$
7: $(1-t)^2$
解説
(1)
$\mathrm{P,Q}$ のとりかたから、 $\overrightarrow{\mathrm{OP}}=(1-t)\vec{a}$ と $\overrightarrow{\mathrm{OQ}}=t\vec{b}$ がわかります。また、
\begin{eqnarray}
\overrightarrow{\mathrm{OR}}
&=&
(1-t)\overrightarrow{\mathrm{OP}}+t\overrightarrow{\mathrm{OQ}} \\[5pt]
&=&
(1-t)^2\vec{a}+t^2\vec{b} \\[5pt]
\end{eqnarray}となります。
解答
アイ:20 (2点)
ウエ:74 (2点)
解答編 つづき
問題
(2) $\mathrm{O,A,B}$ を図1の位置にとる。 $t=\frac{1}{3}$ のときの $\mathrm{R}$ の位置について、図1における点 $\mathrm{R}_0,\mathrm{R}_1,\cdots,\mathrm{R}_9$ のうち正しいものは $\dBox{オ}$ である。ただし、図1における破線は、 $\mathrm{OA}$ を9等分する点を通り $\mathrm{OB}$ に平行な線分と、 $\mathrm{OB}$ を9等分する点を通り $\mathrm{OA}$ に平行な線分である。また、 $\mathrm{R}_0,\mathrm{R}_1,\cdots,\mathrm{R}_9$ は、いずれもこれらの線分どうしの交点である。
$\dbox{オ}$ の解答群
0: $\mathrm{R}_0$
1: $\mathrm{R}_1$
2: $\mathrm{R}_2$
3: $\mathrm{R}_3$
4: $\mathrm{R}_4$
5: $\mathrm{R}_5$
6: $\mathrm{R}_6$
7: $\mathrm{R}_7$
8: $\mathrm{R}_8$
9: $\mathrm{R}_9$
解説
(2)
$t=\frac{1}{3}$ のとき、(1)より\[ \overrightarrow{\mathrm{OR}}=\frac{4}{9}\vec{a}+\frac{1}{9}\vec{b} \]となります。これより、 $\mathrm{OA}$ を $\frac{4}{9}$ 倍した線分と $\mathrm{OB}$ を $\frac{1}{9}$ 倍した線分とを使った平行四辺形を考えれば、 $\mathrm{R}$ は $\mathrm{R}_1$ にあることがわかります。
解答
オ:1 (3点)
解答編 つづき
問題
(3) $0^{\circ}\lt \angle \mathrm{AOB}\lt 90^{\circ}$ の場合を考える。 $\overrightarrow{\mathrm{OC}}=\vec{a}+\vec{b}$ を満たす点 $\mathrm{C}$ をとる。 $\mathrm{O}$ を通り直線 $\mathrm{OC}$ と垂直に交わる直線を $\ell$ とする。 $t$ が $0\lt t\lt 1$ の範囲を動くとき、 $\mathrm{R}$ と $\ell$ の距離について考えよう。
直線 $\mathrm{BC}$ と $\ell$ の交点を $\mathrm{D}$ とし、 $k$ を $\mathrm{OA:BD}=1:k$ を満たす正の数とする。
(i) $\overrightarrow{\mathrm{OD}}$ を $\vec{a},\vec{b}$ と $k$ を用いて表すと\[ \overrightarrow{\mathrm{OD}}=\dBox{カ} \]である。また、直線 $\mathrm{OC}$ と直線 $\mathrm{OD}$ が垂直に交わることから、 $k=\dBox{キ}$ であることがわかる。
$\dbox{カ}$ の解答群
0: $k\vec{a}+\vec{b}$
1: $k\vec{a}-\vec{b}$
2: $-k\vec{a}+\vec{b}$
3: $-k\vec{a}-\vec{b}$
4: $\vec{a}+k\vec{b}$
5: $\vec{a}-k\vec{b}$
6: $-\vec{a}+k\vec{b}$
7: $-\vec{a}-k\vec{b}$
$\dbox{キ}$ の解答群
0: $\dfrac{|\vec{a}|}{|\vec{b}|}$
1: $\dfrac{|\vec{b}|}{|\vec{a}|}$
2: $\dfrac{|\vec{a}|^2+\vec{a}\cdot\vec{b}}{|\vec{b}|^2+\vec{a}\cdot\vec{b}}$
3: $\dfrac{-|\vec{a}|^2-\vec{a}\cdot\vec{b}}{|\vec{b}|^2+\vec{a}\cdot\vec{b}}$
4: $\dfrac{|\vec{b}|^2+\vec{a}\cdot\vec{b}}{|\vec{a}|^2+\vec{a}\cdot\vec{b}}$
5: $\dfrac{-|\vec{b}|^2-\vec{a}\cdot\vec{b}}{|\vec{a}|^2+\vec{a}\cdot\vec{b}}$
解説
(3)
$\overrightarrow{\mathrm{OD}}$ は $\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BD}}$ とかけます。また、 $\mathrm{OA:BD}=1:k$ で、$\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{BD}}$ は平行で向きが異なるので、 $\overrightarrow{\mathrm{BD}}=-k\overrightarrow{\mathrm{OA}}$ となります。これらから、\[ \overrightarrow{\mathrm{OD}}=-k\vec{a}+\vec{b} \]となることがわかります。
直線 $\mathrm{OC}$ と直線 $\mathrm{OD}$ が垂直に交わるので、 $\overrightarrow{\mathrm{OC}}$ と $\overrightarrow{\mathrm{OD}}$ も垂直に交わります。なので、内積は $0$ となります。 $\overrightarrow{\mathrm{OC}}=\vec{a}+\vec{b}$ なので
\begin{eqnarray}
\overrightarrow{\mathrm{OC}} \cdot \overrightarrow{\mathrm{OD}} &=& 0 \\[5pt]
(\vec{a}+\vec{b}) \cdot (-k\vec{a}+\vec{b}) &=& 0 \\[5pt]
-k|\vec{a}|^2 +\vec{a}\cdot\vec{b} -k\vec{a}\cdot\vec{b} +|\vec{b}|^2 &=& 0 \\[5pt]
-k(|\vec{a}|^2+\vec{a}\cdot\vec{b}) &=& -|\vec{b}|^2-\vec{a}\cdot\vec{b} \\[5pt]
k &=& \frac{|\vec{b}|^2+\vec{a}\cdot\vec{b}}{|\vec{a}|^2+\vec{a}\cdot\vec{b}} \\[5pt]
\end{eqnarray}となります。
解答
カ:2 (2点)
キ:4 (2点)
解答編 つづき
問題
(ii) $\vec{c}=\overrightarrow{\mathrm{OC}}$, $\vec{d}=\overrightarrow{\mathrm{OD}}$ とおく。 $\overrightarrow{\mathrm{OR}}$ を、垂直な二つのベクトル $\vec{c},\vec{d}$ と $k,t$ を用いて表すことを考えよう。まず $\vec{a}$ と $\vec{b}$ は、 $\vec{c},\vec{d}$ と $k$ を用いると\[ \vec{a}=\dfrac{1}{k+1}\left(\dBox{ク}\right),\ \vec{b}=\dfrac{1}{k+1}\left(\dBox{ケ}\right) \]と表すことができる。
これから
\begin{eqnarray} \overrightarrow{\mathrm{OR}} &=& \frac{1}{k+1}\left\{\dBox{コ}t^2-\dBox{サ}t+\dBox{シ}\right\}\vec{c} \\[5pt] & & +\frac{1}{k+1}\left(\dBox{ス}-\dBox{セ}\right)\vec{d} \end{eqnarray}であることがわかる。$\dbox{ク},\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\vec{c}+\vec{d}$
1: $\vec{c}-\vec{d}$
2: $-\vec{c}+\vec{d}$
3: $k\vec{c}+\vec{d}$
4: $\vec{c}+k\vec{d}$
$\dbox{コ}$ ~ $\dbox{セ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\frac{1}{2}$
1: $1$
2: $2$
3: $k$
4: $2k$
5: $(k+1)$
6: $2(k+1)$
7: $(k-1)$
8: $2(k-1)$
解説
(ii)
$\vec{c}=\vec{a}+\vec{b}$ と $\vec{d}=-k\vec{a}+\vec{b}$ なので、 $\vec{c}-\vec{d}$ の計算結果を利用すれば
\begin{eqnarray}
\vec{c}-\vec{d} &=& \vec{a}+\vec{b}+k\vec{a}-\vec{b} \\[5pt]
(k+1)\vec{a} &=& \vec{c}-\vec{d} \\[5pt]
\vec{a} &=& \frac{1}{k+1}\left(\vec{c}-\vec{d}\right) \\[5pt]
\end{eqnarray}となります。また、 $k\vec{c}+\vec{d}$ の計算結果を利用すれば
\begin{eqnarray}
k\vec{c}+\vec{d} &=& k\vec{a}+k\vec{b}-k\vec{a}+\vec{b} \\[5pt]
(k+1)\vec{b} &=& k\vec{c}+\vec{d} \\[5pt]
\vec{b} &=& \frac{1}{k+1}\left(k\vec{c}+\vec{d}\right) \\[5pt]
\end{eqnarray}となります。
(1)より、$\overrightarrow{\mathrm{OR}}=(1-t)^2\vec{a}+t^2\vec{b}$ なので、これに先ほどの結果を代入すると
\begin{eqnarray}
\overrightarrow{\mathrm{OR}}
&=&
(1-t)^2\vec{a}+t^2\vec{b} \\[5pt]
&=&
(1-t)^2\frac{1}{k+1}\left(\vec{c}-\vec{d}\right)+t^2\cdot \frac{1}{k+1}\left(k\vec{c}+\vec{d}\right) \\[5pt]
&=&
\frac{1}{k+1}\left\{(1-t)^2+t^2k\right\}\vec{c} \\
& &
+\frac{1}{k+1}\left\{-(1-t)^2+t^2\right\}\vec{d} \\[5pt]
&=&
\frac{1}{k+1}\left\{(k+1)t^2-2t+1\right\}\vec{c} \\
& &
+\frac{1}{k+1}(2t-1)\vec{d} \\[5pt]
\end{eqnarray}となることがわかります。
解答
ク:1 (2点)
ケ:3 (2点)
コサシスセ:52121 (3点)
解答編 つづき
問題
(iii) $t$ が $0\lt t\lt 1$ の範囲を動くとき、 $\mathrm{R}$ と $\ell$ の距離が最小になるのは $t=\dBox{ソ}$ のときである。
$\dbox{ソ}$ の解答群
0: $\dfrac{1}{2}$
1: $\dfrac{1}{k-1}$
2: $\dfrac{2}{k-1}$
3: $\dfrac{1}{k}$
4: $\dfrac{2}{k}$
5: $\dfrac{k-1}{k}$
6: $\dfrac{1}{k+1}$
7: $\dfrac{2}{k+1}$
8: $\dfrac{k-1}{k+1}$
9: $\dfrac{k}{k+1}$
解説
(iii)
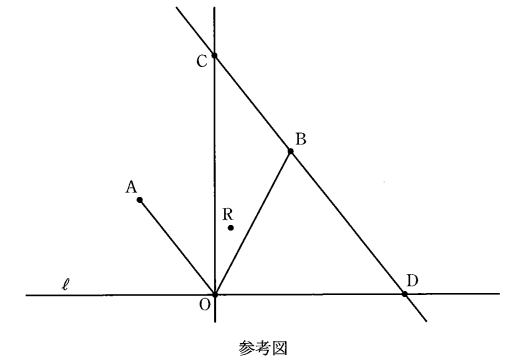
$\mathrm{R}$ から $\ell$ に下した垂線の足を $\mathrm{H}$ とすると、 $\mathrm{R}$ と $\ell$ の距離の最小値は $\mathrm{RH}$ です。 $\mathrm{RH}$ は $\mathrm{OC}$ と平行なので、(ii) の結果の $\vec{c}$ の係数の絶対値の最小値と一致します。つまり、 $\mathrm{R}$ と $\ell$ の距離が最小になる場合を考えるには、(ii) の結果の $\vec{c}$ の係数について考えればいいことがわかります。
係数の部分を計算すると
\begin{eqnarray}
& &
\frac{1}{k+1} \{ (k+1)t^2-2t+1 \} \\[5pt]
&=&
t^2-\frac{2}{k+1}t+\frac{1}{k+1} \\[5pt]
&=&
\left(t-\frac{1}{k+1}\right)^2-\frac{1}{(k+1)^2}+\frac{1}{k+1} \\[5pt]
&=&
\left(t-\frac{1}{k+1}\right)^2+\frac{-1+(k+1)}{(k+1)^2} \\[5pt]
&=&
\left(t-\frac{1}{k+1}\right)^2+\frac{k}{(k+1)^2} \\[5pt]
\end{eqnarray}となります。この値はつねに正で、 $t=\dfrac{1}{k+1}$ のときに最小となることがわかります。また、 $k$ は正の数なので、 $0\lt \dfrac{1}{k+1} \lt 1$ であることがわかります。
よって、 $\mathrm{R}$ と $\ell$ の距離が最小になるのは、 $t=\dfrac{1}{k+1}$ のときだとわかります。
解答
ソ:6 (2点)