共通テスト 数学II・数学B 2024年度追試 第3問 解説

【第3問～第5問から2問選択】

問題編

問題

（正規分布表は省略しています）

　以下の問題を解答するにあたっては、必要に応じて43ページにある正規分布表を用いてもよい。

　太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率 $p$ で「はい」の回答が得られ、確率 $1-p$ で「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。

(1) 1組のグループにおいて、三人のうち一人だけが「はい」と回答する確率を $q$ とする。このとき、 $q$ は $p$ の関数となり、 $q=f(p)$ とおくと\[ f(p)={}_3\mathrm{C}_{\myBox{ア}}p(1-p)^{3-\mybox{ア}} \]であり、 $f\left(\dfrac{1}{3}\right)=\dfrac{\myBox{イ}}{\myBox{ウ}}$ となることがわかる。また、 $0\leqq p\leqq 1$ における関数 $q=f(p)$ のグラフは図1のようになる。

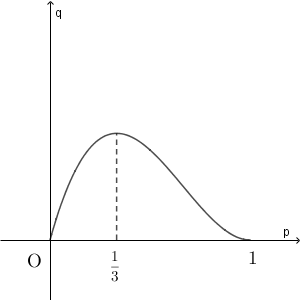
(2) 太郎さんと花子さんは、「質問1」を作成し、試しに三人からなる9組のグループに質問した。その結果が図2に示されており、三人のうち一人だけが「はい」と回答したのは、グループ2とグループ9の2組のグループであった。

図2　9組のグループに質問した結果
〇は「はい」、×は「いいえ」を表す。

グループ1			グループ2			グループ3
×	×	×	〇	×	×	〇	〇	×
グループ4			グループ5			グループ6
〇	×	〇	×	〇	〇	×	〇	〇
グループ7			グループ8			グループ9
〇	〇	〇	〇	×	〇	×	〇	×

　太郎さんと花子さんは、三人のうち一人だけが「はい」と回答したグループの割合が $\dfrac{2}{9}$ となったので、(1)の $q$ を用いて $q=\dfrac{2}{9}$ となる $p$ について考えることにした。 $q=\dfrac{2}{9}$ となる $p$ については、方程式 $f(p)-\dfrac{2}{9}=0$ が\[ \left(p-\frac{\myBox{エ}}{\myBox{オ}}\right)(9p^2-12p+1)=0 \]と変形できることに着目することにより求められる。

(3) 太郎さんと花子さんは、 $p=\dfrac{\mybox{エ}}{\mybox{オ}}$ となるように工夫して「質問II」を考え、今度は三人からなる100個のグループに質問した。その結果、三人のうち一人だけが「はい」と加糖したグループは25組であった。

(i) 太郎さんと花子さんは、「質問II」における(1)の $q$ が $\dfrac{2}{9}$ となるかどうかを回答の結果から確かめることにした。そこで、 $q$ に対する信頼度95%の信頼区間を考えている。

• 三人のうち一人だけが「はい」と回答するグループの数を確率変数として考えてみたらどうかな。
• 二項分布を用いるといいね。

　三人のうち一人だけが「はい」と回答するグループの数を確率変数 $X$ で表すと、 $X$ は二項分布 $B\left(\dBox{カ},q\right)$ に従う。標本の大きさは十分に大きいので、二項分布の正規分布による近似を用いて $q$ に対する信頼度95%の信頼区間を求めることができる。その信頼区間は $0.17\leqq q\leqq 0.33$ となるから、 $\dfrac{2}{9}$ が信頼区間に含まれることが確認できる。

　$\dbox{カ}$ の解答群

　0: $3$
　1: $9$
　2: $25$
　3: $100$
　4: $300$

(ii) 太郎さんと花子さんは、(i)の結果を振り返りながら先生と話をしている。

• 私たちの考えたやり方では、三人のうち一人だけが「はい」と回答するグループの数に着目したね。
• ほかにも方法はないのかな。
• (1)の図1を見たらわかると思うけど、関数 $q=f(p)$ は $\dfrac{1}{3}\leqq p\leqq 1$ で減少するので、 $p$ に対する信頼度95%の信頼区間 $a\leqq p\leqq b$ から、その信頼区間に対応する $q$ のとり得る値の範囲 $c\leqq q\leqq d$ を考えることもできますよ。
• 先生の方法だと、 $q$ のとり得る値の範囲が(i)で求めた $q$ に対する信頼区間よりせまくなるかもしれないね。

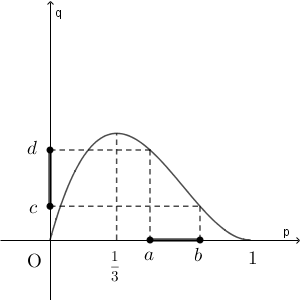
　三人からなる1組のグループに質問するとき、「はい」と回答する人数を確率変数 $Y$ と表すと、 $Y$ は二項分布 $B\left(\dBox{キ},p\right)$ に従う。三人からなる100組のグループに質問するときの結果を、 $Y$ と同じ確率変数をもつ母集団から無作為に抽出した大きさ $n=100$ の標本とみなす。これらを確率変数 $Y_1,Y_2,\cdots,Y_{100}$ で表す。このとき、期待値は\[ E(Y_1)=E(Y_2)=\cdots=E(Y_{100})=\dBox{ク}p \]となる。三人からなる100組のグループから得られた「質問II」への回答結果において、標本平均 $\bar{Y}$ は $1.96$、標本の標準偏差は $0.90$ であった。

　$\dbox{ク}p$ に対する信頼度95%の信頼区間を $L\leqq \dbox{ク}p\leqq U$ とするとき、 $P\left(L\leqq \dbox{ク}p\leqq U\right)=0.95$ である。よって、\[ P\left(\frac{L}{\dbox{ク}}\leqq p\leqq \frac{U}{\dbox{ク}}\right)=0.95 \]となり、 $p$ に対する信頼度95% の信頼区間が求められる。

　標本の大きさが十分に大きいとき、母標準偏差の代わりに標本の標準偏差を用いてよいことが知られているから、 $p$ に対する信頼度95%の信頼区間は $\dBox{ケ}$ となることがわかる。

　$p$ に対する信頼度95%の信頼区間から、先生が示唆した $q$ のとり得る値の範囲は $0.18\leqq q\leqq 0.30$ となる。

　$\dbox{キ},\dbox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $3$
　1: $9$
　2: $25$
　3: $100$
　4: $300$

　$\dbox{ケ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

　0: $0.58\leqq p\leqq 0.73$
　1: $0.59\leqq p\leqq 0.71$
　2: $0.61\leqq p\leqq 0.70$
　3: $0.61\leqq p\leqq 0.76$
　4: $0.63\leqq p\leqq 0.74$
　5: $0.64\leqq p\leqq 0.75$

考え方

(1)は数学IAの範囲で考えられます。(2)はもはや確率の問題でもありません。(3)(i)と(ii)の前半は二項分布に関する簡単な問題です。後半は方針も書いてくれているし、答えを選択肢から選ぶだけ。だいぶ優しいセットになっています。

【第3問～第5問から2問選択】

解答編

問題

（正規分布表は省略しています）

　以下の問題を解答するにあたっては、必要に応じて43ページにある正規分布表を用いてもよい。

　太郎さんと花子さんは、「はい」か「いいえ」のどちらかで答えられる質問を考えている。質問数は一つで、確率 $p$ で「はい」の回答が得られ、確率 $1-p$ で「いいえ」の回答が得られるものとする。この質問を、三人からなるグループの一人ひとりに別々に示し、そのうち一人だけが「はい」と回答する確率を考えたい。

(1) 1組のグループにおいて、三人のうち一人だけが「はい」と回答する確率を $q$ とする。このとき、 $q$ は $p$ の関数となり、 $q=f(p)$ とおくと\[ f(p)={}_3\mathrm{C}_{\myBox{ア}}p(1-p)^{3-\mybox{ア}} \]であり、 $f\left(\dfrac{1}{3}\right)=\dfrac{\myBox{イ}}{\myBox{ウ}}$ となることがわかる。また、 $0\leqq p\leqq 1$ における関数 $q=f(p)$ のグラフは図1のようになる。

解説

(1)
三人のうち「はい」と回答する一人の選び方は ${}_3\mathrm{C}_1$ なので、\[ f(p)={}_3\mathrm{C}_1p(1-p)^{3-1} \]となります。 $p=\dfrac{1}{3}$ を代入すると
\begin{eqnarray} f\left(\frac{1}{3}\right) &=& {}_3\mathrm{C}_1 \cdot \frac{1}{3}\left(1-\frac{1}{3}\right)^{3-1} \\[5pt] &=& 3\cdot \frac{1}{3}\cdot\frac{4}{9} \\[5pt] &=& \frac{4}{9} \\[5pt] \end{eqnarray}と求められます。

解答

ア：1 (2点)
イウ：49 (3点)

解答編　つづき

問題

(2) 太郎さんと花子さんは、「質問1」を作成し、試しに三人からなる9組のグループに質問した。その結果が図2に示されており、三人のうち一人だけが「はい」と回答したのは、グループ2とグループ9の2組のグループであった。

図2　9組のグループに質問した結果
〇は「はい」、×は「いいえ」を表す。

グループ1			グループ2			グループ3
×	×	×	〇	×	×	〇	〇	×
グループ4			グループ5			グループ6
〇	×	〇	×	〇	〇	×	〇	〇
グループ7			グループ8			グループ9
〇	〇	〇	〇	×	〇	×	〇	×

　太郎さんと花子さんは、三人のうち一人だけが「はい」と回答したグループの割合が $\dfrac{2}{9}$ となったので、(1)の $q$ を用いて $q=\dfrac{2}{9}$ となる $p$ について考えることにした。 $q=\dfrac{2}{9}$ となる $p$ については、方程式 $f(p)-\dfrac{2}{9}=0$ が\[ \left(p-\frac{\myBox{エ}}{\myBox{オ}}\right)(9p^2-12p+1)=0 \]と変形できることに着目することにより求められる。

解説

(2)
$f(p)-\frac{2}{9}=0$ を変形すると
\begin{eqnarray} {}_3\mathrm{C}_1 \cdot p(1-p)^{3-1}-\frac{2}{9} &=& 0 \\[5pt] 3p(p^2-2p+1)-\frac{2}{9} &=& 0 \\[5pt] 3p^3-6p^2+3p-\frac{2}{9} &=& 0 \\[5pt] 9p^3-18p^2+9p-\frac{2}{3} &=& 0 \\[5pt] \end{eqnarray}となります。問題文より、これが $9p^2-12p+1$ で割れることを利用して \begin{eqnarray} \left(p-\frac{2}{3}\right)(9p^2-12p+1) &=& 0 \\[5pt] \end{eqnarray}となることがわかります。これより、 $p=\dfrac{2}{3}$ となることもわかります。

解答

エオ：23 (3点)

解答編　つづき

問題

(3) 太郎さんと花子さんは、 $p=\dfrac{\mybox{エ}}{\mybox{オ}}$ となるように工夫して「質問II」を考え、今度は三人からなる100個のグループに質問した。その結果、三人のうち一人だけが「はい」と加糖したグループは25組であった。

(i) 太郎さんと花子さんは、「質問II」における(1)の $q$ が $\dfrac{2}{9}$ となるかどうかを回答の結果から確かめることにした。そこで、 $q$ に対する信頼度95%の信頼区間を考えている。

• 三人のうち一人だけが「はい」と回答するグループの数を確率変数として考えてみたらどうかな。
• 二項分布を用いるといいね。

　三人のうち一人だけが「はい」と回答するグループの数を確率変数 $X$ で表すと、 $X$ は二項分布 $B\left(\dBox{カ},q\right)$ に従う。標本の大きさは十分に大きいので、二項分布の正規分布による近似を用いて $q$ に対する信頼度95%の信頼区間を求めることができる。その信頼区間は $0.17\leqq q\leqq 0.33$ となるから、 $\dfrac{2}{9}$ が信頼区間に含まれることが確認できる。

　$\dbox{カ}$ の解答群

　0: $3$
　1: $9$
　2: $25$
　3: $100$
　4: $300$

解説

(3)
(i)
$1$ となる確率が $q$ で $0$ となる確率が $1-q$ の二項分布を $100$ 個足したものと考えられるので、 $X$ は二項分布 $B(100,q)$ に従うことがわかります。

また、問題文に書いてあることも確認してみます。正規分布表で、\[ P(0\leqq z\leqq z_0)=\frac{0.95}{2}=0.475 \]となっている箇所をみると、 $z_0=1.96$ だとわかります。また、標本比率は $\frac{25}{100}=0.25$ なので、信頼区間は
\begin{eqnarray} & & 0.25-1.96\sqrt{\frac{0.25\cdot 0.75}{100}} \leqq q \leqq 0.25+1.96\sqrt{\frac{0.25\cdot 0.75}{100}} \\[5pt] & & 0.25-1.96\cdot 0.025\sqrt{3} \leqq q \leqq 0.25+1.96\cdot 0.025\sqrt{3} \\[5pt] & & 0.16523 \leqq q \leqq 0.33477 \\[5pt] \end{eqnarray}となります（母標準偏差の代わりに標本の標準偏差を用いています）。問題文にある通り、 $0.17\leqq q\leqq 0.33$ となることがわかります。 $\frac{2}{9}=0.222\cdots$ なので、 $\frac{2}{9}$ がこの信頼区間に含まれることもわかります。

解答

カ：3 (2点)

解答編　つづき

問題

(ii) 太郎さんと花子さんは、(i)の結果を振り返りながら先生と話をしている。

• 私たちの考えたやり方では、三人のうち一人だけが「はい」と回答するグループの数に着目したね。
• ほかにも方法はないのかな。
• (1)の図1を見たらわかると思うけど、関数 $q=f(p)$ は $\dfrac{1}{3}\leqq p\leqq 1$ で減少するので、 $p$ に対する信頼度95%の信頼区間 $a\leqq p\leqq b$ から、その信頼区間に対応する $q$ のとり得る値の範囲 $c\leqq q\leqq d$ を考えることもできますよ。
• 先生の方法だと、 $q$ のとり得る値の範囲が(i)で求めた $q$ に対する信頼区間よりせまくなるかもしれないね。

　三人からなる1組のグループに質問するとき、「はい」と回答する人数を確率変数 $Y$ と表すと、 $Y$ は二項分布 $B\left(\dBox{キ},p\right)$ に従う。三人からなる100組のグループに質問するときの結果を、 $Y$ と同じ確率変数をもつ母集団から無作為に抽出した大きさ $n=100$ の標本とみなす。これらを確率変数 $Y_1,Y_2,\cdots,Y_{100}$ で表す。このとき、期待値は\[ E(Y_1)=E(Y_2)=\cdots=E(Y_{100})=\dBox{ク}p \]となる。三人からなる100組のグループから得られた「質問II」への回答結果において、標本平均 $\bar{Y}$ は $1.96$、標本の標準偏差は $0.90$ であった。

　$\dbox{ク}p$ に対する信頼度95%の信頼区間を $L\leqq \dbox{ク}p\leqq U$ とするとき、 $P\left(L\leqq \dbox{ク}p\leqq U\right)=0.95$ である。よって、\[ P\left(\frac{L}{\dbox{ク}}\leqq p\leqq \frac{U}{\dbox{ク}}\right)=0.95 \]となり、 $p$ に対する信頼度95% の信頼区間が求められる。

　標本の大きさが十分に大きいとき、母標準偏差の代わりに標本の標準偏差を用いてよいことが知られているから、 $p$ に対する信頼度95%の信頼区間は $\dBox{ケ}$ となることがわかる。

　$p$ に対する信頼度95%の信頼区間から、先生が示唆した $q$ のとり得る値の範囲は $0.18\leqq q\leqq 0.30$ となる。

　$\dbox{キ},\dbox{ク}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $3$
　1: $9$
　2: $25$
　3: $100$
　4: $300$

　$\dbox{ケ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

　0: $0.58\leqq p\leqq 0.73$
　1: $0.59\leqq p\leqq 0.71$
　2: $0.61\leqq p\leqq 0.70$
　3: $0.61\leqq p\leqq 0.76$
　4: $0.63\leqq p\leqq 0.74$
　5: $0.64\leqq p\leqq 0.75$

解説

(ii)
$1$ となる確率が $p$ で $0$ となる確率が $1-p$ の二項分布を $3$ 個足したものと考えられるので、 $Y$ は二項分布 $B(3,p)$ に従うことがわかります。

また、 $Y$ の期待値は\[ 3\{1\cdot p+0\cdot(1-p)\}=3p \]となります。

母平均 $3p$ に対する信頼度95%の信頼区間は
\begin{eqnarray} & & 1.96-1.96\cdot\frac{0.90}{\sqrt{100}} \leqq 3p \leqq 1.96+1.96\cdot\frac{0.90}{\sqrt{100}} \\[5pt] & & 1.96-1.96\cdot 0.09 \leqq 3p \leqq 1.96+1.96\cdot 0.09 \\[5pt] & & 1.96 \cdot 0.91 \leqq 3p \leqq 1.96 \cdot 1.09 \\[5pt] \end{eqnarray}となります。これより、 $p$ に対する信頼度95%の信頼区間が求められます。 \begin{eqnarray} \frac{1.96\cdot0.91}{3} &=& 0.5945\cdots \\[5pt] \frac{1.96\cdot1.09}{3} &=& 0.7121\cdots \\[5pt] \end{eqnarray}なので、 $p$ に対する信頼区間は、選択肢から選ぶと\[ 0.59\leqq p\leqq 0.71 \]だとわかります。

解答

キ：0 (2点)
ク：0 (3点)
ケ：1 (5点)