共通テスト 数学II・数学B 2024年度追試 第4問 解説
【第3問~第5問から2問選択】
問題編
問題
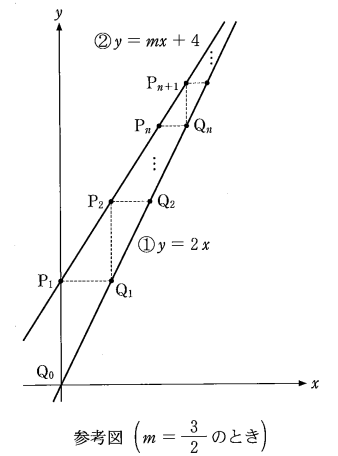
$m$ を $0$ ではない定数とする。座標平面において、2本の直線
\begin{eqnarray} y &=& 2x \quad\cdots ① \\[5pt] y &=& mx+4 \quad\cdots ② \\[5pt] \end{eqnarray}を考える。原点 $(0,0)$ を $\mathrm{Q}_0$, 点 $(0,4)$ を $\mathrm{P}_1$ とし、次の 手順 で点 $\mathrm{Q}_1$, $\mathrm{P}_2$, $\mathrm{Q}_2$, $\cdots$, $\mathrm{P}_n$, $\mathrm{Q}_n$, $\mathrm{P}_{n+1}$, $\cdots$ を定める。
手順
・ $\mathrm{P}_1$ から $x$ 軸に平行な直線を引いて、直線①との交点を $\mathrm{Q}_1$ とする。
・ $\mathrm{Q}_1$ から $y$ 軸に平行な直線を引いて、直線②との交点を $\mathrm{P}_2$ とする。
…
・ $\mathrm{P}_n$ から $x$ 軸に平行な直線を引いて、直線①との交点を $\mathrm{Q}_n$ とする。
・ $\mathrm{Q}_n$ から $y$ 軸に平行な直線を引いて、直線②との交点を $\mathrm{P}_{n+1}$ とする。
…
(1) $m=2$ とする。すなわち、② は $y=2x+4$ である。 $\mathrm{Q}_1$ の座標は $\left(\myBox{ア}, \myBox{イ}\right)$ であり、 $\mathrm{P}_2$ の座標は $\left(\myBox{ウ}, \myBox{エ}\right)$ である。
自然数 $n$ について、 $\mathrm{P}_n$ の $y$ 座標を $a_n$ とする。 $\mathrm{Q}_n$ の $x$ 座標を $a_n$ を用いて表すと、 $\dBox{オ}$ となる。よって、 $\mathrm{P}_{n+1}$ の $y$ 座標 $a_{n+1}$ は $\dBox{カ}$ となる。したがって、数列 $\{a_n\}$ の一般項は $a_n=\dBox{キ}$ である。
$\dbox{オ}$, $\dbox{カ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $2a_n$
1: $a_n-2$
2: $\frac{1}{2}a_n$
3: $\frac{1}{2}a_n-2$
4: $2a_n-4$
5: $2a_n+4$
6: $3a_n-4$
7: $a_n+4$$\dbox{キ}$ の解答群
0: $4n$
1: $2n+2$
2: $6n-2$
3: $2^{n+1}$
4: $2^n+2$
5: $4^n$(2) $m=-1$ とする。すなわち、② は $y=-x+4$ である。自然数 $n$ について、 $\mathrm{P}_n$ の $y$ 座標を $b_n$ とする。
(i) 数列 $\{b_n\}$ について、 $b_1=\myBox{ク}$ かつ\[ b_{n+1}=\dfrac{\myBox{ケコ}}{\myBox{サ}}b_n+\myBox{シ} \ (n=1,2,3,\cdots) \]となる。よって、数列 $\{b_n\}$ の一般項は\[ b_n=\frac{\myBox{ス}}{\myBox{セ}}\left(\frac{\myBox{ソタ}}{\myBox{チ}}\right)^{n-1}+\frac{\myBox{ツ}}{\myBox{テ}} \]となる。
(ii) 自然数 $n$ について、 $\mathrm{Q}_{n-1}$ と $\mathrm{P}_n$ を結ぶ線分の長さを $c_n$ とし、 $\mathrm{P}_n$ と $\mathrm{Q}_n$ を結ぶ線分の長さを $d_n$ とする。 $\mathrm{Q}_0$, $\mathrm{P}_1$, $\mathrm{Q}_1$, $\mathrm{P}_2$, $\mathrm{Q}_2$, $\cdots$, $\mathrm{P}_n$, $\mathrm{Q}_n$ を順に結んだ折れ線の長さを $S_n$ とおく。 $S_n=c_1+d_1+c_2+d_2+\cdots+c_n+d_n$ である。
すべての自然数 $n$ について、 $d_n$ を $c_n$ を用いて表すと、 $d_n=\dBox{ト}$ である。また、数列 $\{c_n\}$ について\[ c_{n+1}=\dBox{ナ} \ (n=1,2,3,\cdots) \]が成り立つ。このことを用いると\[ S_n=\dBox{ニ} \ (n=1,2,3,\cdots) \]となる。
$\dbox{ト}$, $\dbox{ナ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\dfrac{1}{2}c_n$
1: $c_n$
2: $2c_n$
3: $c_n-2$
4: $-\dfrac{1}{2}c_n+4$
5: $-c_n+2$
$\dbox{ニ}$ の解答群
0: $2n+2$
1: $3n+3$
2: $\dfrac{1}{2}n^2+\dfrac{1}{2}n+3$
3: $\dfrac{1}{2}n^2+\dfrac{3}{2}n+4$
4: $4\left\{1-\left(\dfrac{1}{2}\right)^{n-1}\right\}$
5: $6\left\{1-\left(\dfrac{1}{2}\right)^{n-1}\right\}$
6: $8\left\{1-\left(\dfrac{1}{2}\right)^{n}\right\}$
7: $12\left\{1-\left(\dfrac{1}{2}\right)^{n}\right\}$
考え方
漸化式を求めて、一般項を求めて、和を求める。よくある流れです。図形もシンプルなので、迷うことはないでしょう。(2)は参考図とは違って右下がりのグラフが出てくることに注意しましょう。最後は図形的に考えて式を作ってもいいし、計算式を使って求めてもかまいません。
【第3問~第5問から2問選択】
解答編
問題
$m$ を $0$ ではない定数とする。座標平面において、2本の直線
\begin{eqnarray} y &=& 2x \quad\cdots ① \\[5pt] y &=& mx+4 \quad\cdots ② \\[5pt] \end{eqnarray}を考える。原点 $(0,0)$ を $\mathrm{Q}_0$, 点 $(0,4)$ を $\mathrm{P}_1$ とし、次の 手順 で点 $\mathrm{Q}_1$, $\mathrm{P}_2$, $\mathrm{Q}_2$, $\cdots$, $\mathrm{P}_n$, $\mathrm{Q}_n$, $\mathrm{P}_{n+1}$, $\cdots$ を定める。
手順
・ $\mathrm{P}_1$ から $x$ 軸に平行な直線を引いて、直線①との交点を $\mathrm{Q}_1$ とする。
・ $\mathrm{Q}_1$ から $y$ 軸に平行な直線を引いて、直線②との交点を $\mathrm{P}_2$ とする。
…
・ $\mathrm{P}_n$ から $x$ 軸に平行な直線を引いて、直線①との交点を $\mathrm{Q}_n$ とする。
・ $\mathrm{Q}_n$ から $y$ 軸に平行な直線を引いて、直線②との交点を $\mathrm{P}_{n+1}$ とする。
…
(1) $m=2$ とする。すなわち、② は $y=2x+4$ である。 $\mathrm{Q}_1$ の座標は $\left(\myBox{ア}, \myBox{イ}\right)$ であり、 $\mathrm{P}_2$ の座標は $\left(\myBox{ウ}, \myBox{エ}\right)$ である。
自然数 $n$ について、 $\mathrm{P}_n$ の $y$ 座標を $a_n$ とする。 $\mathrm{Q}_n$ の $x$ 座標を $a_n$ を用いて表すと、 $\dBox{オ}$ となる。よって、 $\mathrm{P}_{n+1}$ の $y$ 座標 $a_{n+1}$ は $\dBox{カ}$ となる。したがって、数列 $\{a_n\}$ の一般項は $a_n=\dBox{キ}$ である。
$\dbox{オ}$, $\dbox{カ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $2a_n$
1: $a_n-2$
2: $\frac{1}{2}a_n$
3: $\frac{1}{2}a_n-2$
4: $2a_n-4$
5: $2a_n+4$
6: $3a_n-4$
7: $a_n+4$$\dbox{キ}$ の解答群
0: $4n$
1: $2n+2$
2: $6n-2$
3: $2^{n+1}$
4: $2^n+2$
5: $4^n$
解説
(1)
$\mathrm{Q}_1$ の $y$ 座標は $\mathrm{P}_1$ の $y$ 座標と同じ $4$ です。また、点 $\mathrm{Q}_1$ は $y=2x$ 上にあるので、 $x$ 座標は $2$ です。よって、 $\mathrm{Q}_1$ の座標は $(2,4)$ です。
$\mathrm{P}_2$ の $x$ 座標は $\mathrm{Q}_1$ の $x$ 座標と同じ $2$ です。また、点 $\mathrm{P}_2$ は $y=2x+4$ 上にあるので、 $y$ 座標は $8$ です。よって、 $\mathrm{P}_2$ の座標は $(2,8)$ です。
$\mathrm{Q}_n$ の $y$ 座標は $\mathrm{P}_n$ の $y$ 座標と同じ $a_n$ です。また、点 $\mathrm{Q}_n$ は $y=2x$ 上にあるので、 $x$ 座標は $\frac{1}{2}a_n$ です。
$\mathrm{P}_{n+1}$ の $x$ 座標は $\mathrm{Q}_n$ の $x$ 座標と同じ $\frac{1}{2}a_n$ です。また、点 $\mathrm{P}_{n+1}$ は $y=2x+4$ 上にあるので、 $y$ 座標は $2\cdot \frac{1}{2}a_n+4=a_n+4$ です。
これより、漸化式 $a_{n+1}=a_n+4$ が得られました。数列 $\{a_n\}$ は、初項が $4$ で公差が $4$ の等差数列なので、一般項は $a_n=4n$ と求められます。
解答
アイ:24 (1点)
ウエ:28 (1点)
オ:2 (2点)
カ:7 (2点)
キ:0 (2点)
解答編 つづき
問題
(2) $m=-1$ とする。すなわち、② は $y=-x+4$ である。自然数 $n$ について、 $\mathrm{P}_n$ の $y$ 座標を $b_n$ とする。
(i) 数列 $\{b_n\}$ について、 $b_1=\myBox{ク}$ かつ\[ b_{n+1}=\dfrac{\myBox{ケコ}}{\myBox{サ}}b_n+\myBox{シ} \ (n=1,2,3,\cdots) \]となる。よって、数列 $\{b_n\}$ の一般項は\[ b_n=\frac{\myBox{ス}}{\myBox{セ}}\left(\frac{\myBox{ソタ}}{\myBox{チ}}\right)^{n-1}+\frac{\myBox{ツ}}{\myBox{テ}} \]となる。
解説
(2)
(i)

$\mathrm{P}_1$ の $y$ 座標は $4$ なので、 $b_1=4$ です。
$\mathrm{Q}_n$ の $y$ 座標は $\mathrm{P}_n$ の $y$ 座標と同じ $b_n$ です。また、点 $\mathrm{Q}_n$ は $y=2x$ 上にあるので、 $x$ 座標は $\frac{1}{2}b_n$ です。
$\mathrm{P}_{n+1}$ の $x$ 座標は $\mathrm{Q}_n$ の $x$ 座標と同じ $\frac{1}{2}b_n$ です。また、点 $\mathrm{P}_{n+1}$ は $y=-x+4$ 上にあるので、 $y$ 座標は $-1\cdot \dfrac{1}{2}b_n+4=-\dfrac{1}{2}b_n+4$ です。
これより、漸化式 $b_{n+1}=-\frac{1}{2}b_n+4$ が得られました。 $p=-\frac{1}{2}p+4$ とすると $p=\frac{8}{3}$ となることから
\begin{eqnarray}
b_{n+1}-\frac{8}{3} &=& -\frac{1}{2}\left(b_n-\frac{8}{3}\right) \\[5pt]
b_n-\frac{8}{3} &=& \left(-\frac{1}{2}\right)^{n-1} \left(b_1-\frac{8}{3}\right) \\[5pt]
&=& \left(-\frac{1}{2}\right)^{n-1} \left(4-\frac{8}{3}\right) \\[5pt]
&=& \left(-\frac{1}{2}\right)^{n-1} \cdot \frac{4}{3} \\[5pt]
b_n &=& \frac{4}{3} \left(-\frac{1}{2}\right)^{n-1} +\frac{8}{3} \\[5pt]
\end{eqnarray}と求められます。
解答
クケコサシ:4-124 (2点)
スセソタチツテ:43-1283 (3点)
解答編 つづき
問題
(ii) 自然数 $n$ について、 $\mathrm{Q}_{n-1}$ と $\mathrm{P}_n$ を結ぶ線分の長さを $c_n$ とし、 $\mathrm{P}_n$ と $\mathrm{Q}_n$ を結ぶ線分の長さを $d_n$ とする。 $\mathrm{Q}_0$, $\mathrm{P}_1$, $\mathrm{Q}_1$, $\mathrm{P}_2$, $\mathrm{Q}_2$, $\cdots$, $\mathrm{P}_n$, $\mathrm{Q}_n$ を順に結んだ折れ線の長さを $S_n$ とおく。 $S_n=c_1+d_1+c_2+d_2+\cdots+c_n+d_n$ である。
すべての自然数 $n$ について、 $d_n$ を $c_n$ を用いて表すと、 $d_n=\dBox{ト}$ である。また、数列 $\{c_n\}$ について\[ c_{n+1}=\dBox{ナ} \ (n=1,2,3,\cdots) \]が成り立つ。このことを用いると\[ S_n=\dBox{ニ} \ (n=1,2,3,\cdots) \]となる。
$\dbox{ト}$, $\dbox{ナ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\dfrac{1}{2}c_n$
1: $c_n$
2: $2c_n$
3: $c_n-2$
4: $-\dfrac{1}{2}c_n+4$
5: $-c_n+2$
$\dbox{ニ}$ の解答群
0: $2n+2$
1: $3n+3$
2: $\dfrac{1}{2}n^2+\dfrac{1}{2}n+3$
3: $\dfrac{1}{2}n^2+\dfrac{3}{2}n+4$
4: $4\left\{1-\left(\dfrac{1}{2}\right)^{n-1}\right\}$
5: $6\left\{1-\left(\dfrac{1}{2}\right)^{n-1}\right\}$
6: $8\left\{1-\left(\dfrac{1}{2}\right)^{n}\right\}$
7: $12\left\{1-\left(\dfrac{1}{2}\right)^{n}\right\}$
解説
(ii)

三角形 $\mathrm{Q}_{n-1}\mathrm{P}_n\mathrm{Q}_n$ について考えると、縦の長さ $c_n$ を横の長さ $d_n$ で割ったものは、② の傾き $2$ と一致します。なので、\[ d_n=\frac{1}{2}c_n \]とわかります。
また、三角形 $\mathrm{P}_n\mathrm{Q}_n\mathrm{P}_{n+1}$ について考えると、縦の長さ $c_{n+1}$ を横の長さ $d_n$ で割ったものは、② の傾き $-1$ の絶対値と一致します。なので、\[ c_{n+1}=d_n \]となります。よって、先ほど求めたことと合わせて
\begin{eqnarray}
c_{n+1} &=& d_n=\frac{1}{2}c_n
\end{eqnarray}となります。
$c_1=|b_1-b_0|=4$ なので、数列 $\{c_n\}$ は初項が $4$ で公比が $\dfrac{1}{2}$ の等比数列なので、\[ c_n=4\cdot \frac{1}{2^{n-1}}=\frac{1}{2^{n-3}} \]となります。
よって
\begin{eqnarray}
S_n
&=&
c_1+d_1+c_2+d_2+\cdots+c_n+d_n \\[5pt]
&=&
c_1+\frac{1}{2}c_1+c_2+\frac{1}{2}c_2+\cdots+c_n+\frac{1}{2}c_n \\[5pt]
&=&
\frac{3}{2}(c_1+c_2+\cdots+c_n) \\[5pt]
&=&
\frac{3}{2} \sum_{k=1}^n\frac{1}{2^{k-3}} \\[5pt]
&=&
\frac{3}{2}\cdot\frac{4\left(1-\frac{1}{2^n}\right)}{1-\frac{1}{2}} \\[5pt]
&=&
12\left\{1-\left(\dfrac{1}{2}\right)^{n}\right\}
\end{eqnarray}と求められます。
ちなみに、 $n=1$ のときに $4+2=6$ となることはすぐにわかりますが、選択肢を見るとこの時点で大半が消えます。特に、4と5は $n=1$ とすると $0$ になってしまうので、正解のはずがないです。
解答
ト:0 (2点)
ナ:0 (2点)
ニ:7 (3点)





